This blog is a response to Dan Linford's response to my response to Linford's Neo-Lorentzian Relativity and the Beginning of the Universe. I am grateful that Linford took the time to respond to my obscure blog, and I also appreciate Joseph Schmid from the Majesty of Reason blog for hosting Linford's response. Admittedly, my writing may have been a loose, baggy monster to navigate, and I sympathize with the effort that Linford exerted to find points worth commenting on.
I apologize for how long it takes for me to write these responses, but due to family obligations, I can't find the time to write these things with the speed I'd prefer. As my kids grow older, my time should start freeing up and I can start to contribute here more and on YouTube. The good news is that I have finally finished Philipp Roser's Gravitation and Cosmology with York Time, thought about it, and I believe now more than ever that York Time poses absolutely no threat to the past-finitude of the universe. In fact, I think this is so obvious that I'm baffled as to why anyone, let alone Linford, would think that it's a serious rival to Cosmic Time for identifying the preferred foliation (the CMC foliation). Thus, Linford says:
I argue that Craig and company have not adequately defended a measure of past absolute time. While Craig and company have identified cosmic time with absolute time, there is another candidate for absolute time — the York time — that, while answering to many similar motivations as cosmic time, places the Big Bang infinitely far into the past. Furthermore, I identify some reasons that York time might be thought to be a superior candidate for absolute time. Thus, unless Craig and company can adequately motivate cosmic time as an alternative to York time, Big Bang theory provides advocates of absolute time no good reason for endorsing the KCA’s second premise.
Based on my reading of Roser, to say that York Time places the Big Bang infinitely far into the past, while true in a sense, is also extremely misleading, and that a proper interpretation of this idea renders York Time completely harmless as a rival to Cosmic Time for labeling the CMC foliation. Moreover, Linford's saying that Craig has identified cosmic with absolute time isn't exactly true (it's a physical measure of absolute time; it approximates it). Also, Linford's take on why Craig's opting for cosmic time doesn't break the symmetry between cosmic and York time is completely undercut when York time is seen in its proper context. (Again, let the reader be aware: I know I'm not even close to being an expert in these areas and I will argue for these points in a spirit of bewildered trepidation since I'm truly confused about Linford's confidently thinking that York Time poses any kind of a threat to the Kalam. But not to worry, I will take the necessary steps to show the reader exactly where I'm coming from in the blog, and I am convinced - at the moment - that Linford has seriously misunderstood York Time's cosmological consequences ).
York Time takes up the second part of Linford's blog.
In the first part, Linford will defend his 'schema' for successfully building a scientific case that the universe began to exist. Linford thinks it's only a case for the past-finitude of the (observable) universe, but because I completely disagree with Linford's modal case for thinking that the universe's past-finitude doesn't imply its beginning to exist, I'm going to go ahead and call it a schema for building such a case for the universe's beginning to exist.
In the third part, Linford once more takes his stand on why Neo-Lorentzianism implies a skepticism that undercuts using scientific evidence to support the plausibility of the universe's beginning to exist. I stand by many of the previous comments I made about Linford's skepticism, so I'll be responding to Linford's response to those comments below.
-----------------------------------------------
1. Some Notes on Linford's Introduction
a. I'm ambivalent about the moral Linford seems to be drawing from James Playfair's account of geologist James Hutton's idea of Deep Time and what happened at Siccar Point. I agree that demonstrable science plausibly outweighs unfounded religious dogmatism. I also realize that demonstrable science can lead Reason to wonders that Imagination couldn't have dreamt of. But this particular paradigm shift was against the backdrop of interpreting the Bible's chronology literally (and therefore incorrectly). Since that interpretation guided their geological paradigm, I agree that Deep Time was a jarring shift. But the shift had nothing to do with falsifying the Bible's chronology; it had to do with falsifying a particular interpretation of that chronology. If the geologists that Hutton had brought to Siccar Point hadn't been dominated by that particular interpretation, then Deep Time would have been met with an entirely different reaction. The scientific advance would have had nothing to do with the controversy of science versus religion but would have been a pure, scientific delight for people whose worldviews were amenable to such advances. It would have been one more discovery that the tools of science had blessed us with to know more about the world God created. It would have had as benign an effect on such a worldview as the discovery of penicillin or the invention of the lightbulb. (For a circumspect history of Geology and the Bible, I recommend The Bible, Rocks and Time: Geological Evidence for the Age of the Earth by Davis A. Young and Ralph F. Stearley).
So, what is the parallel supposed to be? Is it this? Just as Hutton's idea of Deep Time shattered the geological paradigm of Bible-believing Christians, so a proper understanding of the content and ramifications of Relativistic Cosmology will shatter the cosmological paradigm of Natural Theologians that appeal to Big Bang Cosmology to establish that the universe began to exist? Of course, I deny the parallel, which you'd expect, but the rhetorical winds of the anecdote don't blow by me unnoticed, and, hopefully, unsuspecting readers aren't taken in too much by it, despite its poignancy. Peradventure, this blog will act as a counterbalance.
b. "the argument [Kalam] does not explicitly mention God and should have broad interest" (Linford) - First, I appreciate this point on a certain level. Outside Natural Theology, thinking about the argument by itself, it is intriguing to think that if the first two premises hold, then the universe has a cause for its coming into existence at some point in the finite past. And if the argument is sound, it can serve as a pillar in a scientific research program that seeks to make testable predictions within these parameters. The causal principle is interesting in itself. The debate about the nature of time is fascinating. Infinity is an ocean that could take a lifetime to sail. So, I share Linford's sentiments on this score.
Second, I want the reader to be aware that sometimes the explicit absence of 'God' from the conclusion of the argument doesn't mean anything dialectically alarming or deficient. Suppose there was an argument A for the conclusion that the tallest person in Cleveland, Ohio loves raw oysters: the tallest person in Cleveland, Ohio is a huge fan of all things seafood and whoever is a huge fan of all things seafood loves raw oysters. Q.E.D. And suppose that Shaquille O'Neal lived in Cleveland, Ohio and no one in Cleveland was taller than him. Thus, while A doesn't explicitly mention Shaquille O'Neal, A nevertheless is an argument for Shaquille O'Neal being a lover of raw oysters. There would need to be additional sub-reasons connecting the definite description to what that description rigidly designates. The same thing is going on in Kalam's conclusion. The definite description 'cause of the universe' rigidly designates God (or, as Aquinas might put it, what everyone means by God), or so the sub-reasons argue.
c. "I doubt premise 1 because premise 1 conflicts with a family of theories concerning the nature of causation (causal republicanism) that I find attractive" (Linford) -
Roughly, the moniker "Causal Republicanism" derives from a political metaphor about causation in response to Bertrand Russell's jab that causation was like the Monarchy: "...a relic of a bygone age, surviving, like the monarchy, only because it is erroneously supposed to do no harm." In response, Causal Republicanism doesn't get rid of causation altogether, but it does think it is absent (or mostly absent) in the realm of Physics, and where it does apply, it is 'constructed by us'. The power of causation, so to speak, is a power that we give it, just as the power of rulers in a Republican Government derives from our vote.
The problem with addressing this here is that since the view isn't monolithic, it would take me too far afield to address it in all its different varieties. Moreover, I'm wondering what these philosophers of physics mean by causation. With this in mind, I have at least three reasons for not being presently convinced by Causal Republicanism.
First, I again mention William Lane Craig's comment about causation in his first rebuttal to Sean Carroll as a conceptual parameter, a parameter I'm in agreement with: "There is no analysis given of what it means to be a cause in this first premise. You can adopt your favorite theory of causation or take causation to be a conceptual primitive." So, what these philosophers of physics need to do for me is to tell me what it is that doesn't exist in physics, and then demonstrate that this thing is what causation essentially amounts to and that it is this thing that you won't find in physics. The problem with this route is that it seems to fall prey to what Peter van Inwagen has called verbal essentialism, the idea that the word causation can only mean one thing and that whatever doesn't amount to that thing doesn't get to be the referent of the word 'causation'. This seems unavoidably ad hoc. Causal Republicanism seems like it needs to do something like this; otherwise, I'm not sure how it can circumscribe what it is that doesn't exist in physics and that whatever this is is essentially what causation is.
Second, I was led to my view of causation from a wonderful and lesser-known book called Theories of Causality: From Antiquity to the Present by John Losee, who provides an extremely helpful "flowchart for assessing causal relatedness", and a "taxonomy of causal attributions" that is so fine-grained that you have to wonder what it is that the Causal Republicans need causation to be in order for physics to have no room for it! To add to the political metaphors, I call my view Causal Timocracy, the idea that there are a variety of kinds of phenomena that have the honor of standing in a particular relation of causal relatedness, and therefore there being an instance of causation. While the book doesn't explicitly have a view called Causal Republicanism, it does address Russell's view (which overlaps with it), along with J.J.C. Smart's "anti-causalism".
My third reason is something that needs more unpacking, but it definitely deserves mention, and it needs to be kept in the background. Banishing causation from physics would mean (if it's true that whatever begins to exist has a cause) that nothing begins to exist in physics. Well, right! If things begin to exist in physics, there's no way physics could banish causation from its domain. The reason things can't begin to exist in physics, and therefore why there is no causation at that level of description/explanation, is because (as Craig notes) the language of physics is purged of all tense. Physics has no room for A-theoretic properties. You can find this in The Tenseless Theory of Time, where Craig explains how Special Relativity presumably abolished metaphysical time by reducing it to empirical measures, or 'physical time'. This physical time, symbolized by 't' in relativistic equations, is far removed from our intuitive understanding of time and Craig substantiates this when he discusses Carlo Rovelli's study of the physical time concept, which is starkly different from the metaphysical time that A-theorists endorse. Rovelli identifies "eight characteristics commonly associated with time," providing a chart that highlights the diversity of the physical time concept, leading Craig to conclude:
"It is difficult to resist the conclusion that all of these operationally defined "times" are not really time at all, but just various measures of time suitable for their respective fields of inquiry. The reductio ad absurdum of the positivistic reduction of time to its measures is surely the conclusion of someone like Barbour that because time in quantum gravity disappears, therefore time does not exist!"
[One wonders if this is the metaphysically benign sense in which the universe was fundamentally a nonspatiotemporal thing, from which its spatiotemporal properties emerged (?) and, if it is, how unlike and disanalogous it is to the metaphysically robust sense in which it is said that sans the universe altogether, God is timeless.]
So, it's, again, misleading for Linford to say (in the blog response):
"Time went from being an entity beyond scientific examination to being an object of scientific study in its own right; with time as an object of scientific study in its own right, there opened the possibility that science could infer that time had a beginning."
The concept of 'time' within quantum gravity presents a compelling irony, as mentioned by Linford in the abstract of his paper "A Modal Condition for the Beginning of the Universe". He observes that according to numerous quantum gravity theories or interpretations of quantum theory, space-time isn't deemed fundamental to physical reality. Instead, it can be explained in terms of more fundamental physical substructures. But it's crucial to remember that if Linford equates the 'time' in quantum theory with the 'time' that God exists outside of in His timeless stage, it's a misguided assumption. Quantum gravity theories only contain the concept of physical time. However, the universe could still be temporal from the perspective of metaphysical time, meaning it's not 'timeless' in the way God is, considering this attribute is contingent. Hopefully, Linford will address this nuanced point. If he doesn't, his arguments may lack the required precision. As I will demonstrate later, disregarding the distinction between physical and metaphysical time can lead to some non-sequiturs about what ensues from God's having a "first finitely long period in the life of physical reality" and the universe (or Cosmos) experiencing such a period.
d. "Some philosophically sophisticated proponents of the KCA have argued that beginning to exist requires a tensed theory of time; moreover, they have argued that, in light of the empirical success of relativistic physics, friends of a tensed theory of time ought to accept a Neo-Lorentzian alternative to Special Relativity and an instrumentalist interpretation of General Relativity."
In this blog, I will continue to express my dissatisfaction with the wording here. I will continue to assert (and I will explain this more below) that neither Craig nor I am an instrumentalist when it comes to the theory of General Relativity. And I also affirm that neither Craig nor I accept a Neo-Lorentzian alternative to Special Relativity. I continue to be bewildered as to why Linford frames it this way. What Craig and myself are instrumentalists about is not General Relativity, but this metaphysical entity called Spacetime that the gatekeepers of GR keep identifying it with, such that if you deny the existence of spacetime, you deny the ontological commitments that being a GR realist commits you too.
As I read through Linford's response, I was disappointed that he didn't interact with what I said on this score. This was the conceptual issue we ran into when we first broached the issue on voice chat. There had been confusion with the way I had expressed what turned out to be a correct conceptual distinction involved with expressing a scientific theory: the mathematical formalism of the theory and the physical interpretation of that formalism. GR is essentially the formalism. Craig agrees with this formalism as far as I know. I take a little bit of a different route. I will argue later that GR may be able to be formulated differently, but that even if you stick with Einstein's original formalism, this poses no threat to Neo-Lorentzianism if the Neo-Lorentzian is an anti-realist about the existence of spacetime; it is at that point that Neo-Lorentzians physically interpret the formalism differently than the spacetime realists do. (Below I will elaborate more on why it's not necessary for Neo-Lorentzians to alter that formalism to accommodate the introduction of forces.)
And the same can be said for Special Relativity. Lorentz endorsed the formalism of SR (along with its kinematic effects), but rejected Einstein's physical interpretation of that formalism (along with Einstein's physical interpretation of those kinematic effects). To call Lorentz's approach an alternative to SR is very misleading to me. The heart of SR is the Lorentz transformation equations. If we accept Linford's framing here, Lorentz and Neo-Lorentzians would be accepting an 'alternative' to the Lorentz transformation equations (?), which is conceptually absurd. What Neo-Lorentzians affirm is that there's nothing about the formalism of SR that does anything to shave away Absolute Time and that there are good reasons for rejecting the existence of spacetime.
A final point is that there's nothing about Neo-Lorentzianism in itself that mandates a Tensed Theory of Time, and there's nothing about a Tensed Theory of Time that mandates Neo-Lorentzianism. And I'm not sure where Craig argues that if time is tensed, then you ought to subscribe to Neo-Lorentzianism. As everyone knows, Einstein's original physical interpretation of SR, prior to Minkowski's spacetime, was tensed, but he did not subscribe to Absolute Time, a pillar of Neo-Lorentzianism. And, as Craig has pointed out in multiple places, it's entirely possible to be a Neo-Lorentzian and endorse the existence of spacetime! You could incorporate tense into spacetime by specifying a preferred foliation; this position is probably consistent with a Moving Spotlight Theory of temporal becoming, which analogizes Time to a Spotlight dynamically moving along a static, four-dimensional spacetime background. Of course, in this case, physical time, as part of that four-dimensional continuum, would be distinct from the tensed, metaphysical time identified as the 'moving spotlight'. Perhaps there's a normative point that is going over my head. But I digress.
e. "Damore’s post is riddled with confusions and technical/mathematical errors that make his post difficult to respond to in entirety, particularly given my limited time constraints."
Of course, Linford is free to think this, and while I am always open to correction, to say that my blog was 'riddled' with such "confusions" is a bit hyperbolic to me. When Linford's corrections came, I often found that Linford either misunderstood what I was saying or that the nature of the issue was at such a high level of abstraction, my expressions or concerns were either not that wide of the mark (and were, at worst, expressed infelicitously) or are points of contention themselves. We both know the exasperation felt when critique is conflated with misunderstanding, with the corollary that understanding means assenting. I'll point this out as it comes up. But I'll also admit the legitimate errors Linford helped correct.
While I definitely appreciate Linford's expertise in the philosophy of physics and his technical competence in the mathematics of these areas, along with these gracious remarks about calling me a friend and his willingness to help me in this public venue, I've found that a lot of these 'corrections' haven't yet (it seems to me) scratched the itch I'm trying to call attention to. Most of the time, I feel like a pupil indulging his professor's explanation of my errors, but that my initial questions don't feel like they're being addressed. I don't mean this to be insulting at all. I mention it to give the reader some balance to how Linford is appraising the quality of my critique.
The professorial metaphor is compounded by Linford's list of book recommendations to help my ignorance of relativity. For example, Linford recommends Sean Carroll’s The Biggest Ideas in the Universe, which is an awesome book. I find Carroll refreshingly clear and he singlehandedly dusted off some of the cobwebs I had when it comes to understanding the math. But there's absolutely nothing in this book that addresses my specific questions. The chapter 'Geometry' was neat and informative, but it did nothing to interact with the criticisms of reducing physics to geometry or the geometric approach leading to the existence of spacetime. I'm at the point where I want the gatekeepers to interact with criticism so that I can make up my own mind. It's the same for Tim Maudlin’s Philosophy of Physics: Space and Time; the chapter 'Special Relativity' literally has a section called 'Special Relativity and Minkowski Space-Time'; but I'm already aware of that entire story and why they tell it the way they do. I want to hear what critics of this story have to say. The same can be said for the rest of Linford's list of book recommendations. If Linford were completely ignorant about the literature on the Kalam, for example, I wouldn't only give him Craig, Moreland, Loke, Erasmus, Oderberg, and Koons; I would also give him Oppy, Sobel, Morriston, Malpass, Pitts, and Smith.
-------------------------------------------------------------
2. Linford's General Schema for Using Scientific Evidence to Infer that the Universe Began to Exist
a. “I defended in my doctoral dissertation and in a subsequent article published in Erkenntnis, showing that the Universe has a finite age is neither necessary nor sufficient for showing that the Universe began to exist. However, Craig and company disagree; on their view, if the Universe has a finite age, then, provided the truth of a tensed theory of time, the Universe did begin to exist. In this post, I will play along and assume their definition” (Linford).
Just so the reader is aware, Linford’s disagreement was touched on above. Linford thinks that if the universe’s spatiotemporality isn’t fundamental, then, at a fundamental level, the universe is not spatiotemporal; and if the universe is not temporal, at that level, then, prior to the emergence of spacetime, the universe has a ‘timeless’ (non-spatiotemporal) stage of existence. But God has a ‘timeless’ stage of existence and had a first temporal stage of existence (simultaneous with His creation of the world). But just as I wouldn't want to say that God, therefore, began to exist if God had a first temporal stage of existence, then Linford argues that I shouldn't say that the universe began to exist if the universe had a first temporal stage of its existence, and thus a finite age. Therefore, having a finite age doesn't imply that you began to exist.
As I touched on above, Linford’s argument is undercut by the fact that the universe wouldn’t be timeless in the same sense that God is timeless sans creation. The non-fundamentality of the universe’s ‘temporal properties’ have to do with ‘physical time’, not ‘metaphysical time’. God’s timelessness has to do with the latter. Physical time is a ‘measure’ of metaphysical time.
Second, since Craig thinks that change is sufficient, and perhaps necessary, for metaphysical time, and since quantum states are inherently unstable, it follows that quantum states involve incessant change on that fundamental level. Thus, even if the relevant physical time hasn’t yet emerged, there is another kind of physical time on the quantum level, and so the universe still always had time at the fundamental level. The same cannot be said for God. As an immaterial being, God’s ontology doesn’t involve quantum instability at all. God’s simplicity makes it entirely possible to conceive God as timeless sans creation, neither admitting of metaphysical time nor any of its measures. Any change in God’s being would admit metaphysical time, rendering God temporal relative to that change. Craig’s example of God’s having a timeless intention to count down from, say, 5 causally prior to creation, and then beginning such a countdown, means that God became metaphysically temporal causally prior to becoming, simultaneous with creation, temporally related to the universe, due to God’s extrinsically changing relationship with respect to the creation of the universe, which is inherently (on any level of description) an object subject to change.
More can be said, and Linford has said much more in his essay, but let the following schema suffice for now. For any object O, including the universe, if O does not have a metaphysically timeless stage of existence, it follows that O’s first, metaphysically temporal stage of existence signals O’s coming into being at that state of existence, and so for all O's not having a metaphysically timeless stage of existence, if O has a finite age, then O began to exist. Any first, 'physically' temporal stage of existence would be a 'measure' of a metaphysically temporal stage of existence, and so such a physically temporal stage would suffice for a metaphysically temporal stage, thus satisfying the schema for determining when O's finite age implies O's beginning to exist.
b. Linford’s Schema: “To infer that U has a finite age, we need a well-confirmed scientific theory T, such that we ought to endorse a realistic interpretation of T and such that T, together with observations, implies U has a finite age.”
Also Linford: “... scientists have made the inference that the observable universe — that is, the largest spacetime region empirically available to us — has a finite age. For all that scientists have said, there could be spatiotemporal regions that either preceded the observable universe or that are beyond our cosmological horizon; those other regions could be infinitely old, indeterminately old, or otherwise different in age from the observable universe.”
Also Linford: “My schema is motivated by noting that whether U [‘either the Universe or the Observable Universe’] had an origin in the finite past is not directly observable. However, philosophers of science have long maintained that if we are right to adopt a realistic interpretation of a given scientific theory, then we can use that theory, in conjunction with observations, to infer the existence of unobservable entities, relations, or phenomena.”
First, Linford’s schema seems too strong the more I think about it. Since science deals with probabilities, all we should be expected to say (and Craig speaks like this ubiquitously in the literature) is that, when considering the available scientific evidence, it is ‘probably the case that’ or it is ‘plausible’ (more plausibly true than its denial, he’d say) that U has a finite age, and so it is probable (or more plausible than not) that U began to exist. Of course, there are deductive as well as inductive ‘inferences’, but Linford’s use of the word ‘implies’ seems to indicate a deduction of sorts. But if it’s an induction, Linford’s talking about the possibility of spatiotemporal regions beyond our cosmological horizon is irrelevant, since such possibilities not only have no positive evidence in their favor (that I’m aware of) but are less probable/plausible than what it is we do have positive evidence in favor of.
Second, this neo-Kantian bifurcation between 'the universe' and 'the observable universe' doesn’t entail anything epistemically catastrophic for me. Perhaps I'm epistemically naive here. I take the “inference that the observable universe — that is, the largest spacetime region empirically available to us — has a finite age” to be an adequate approximation of the finite age of “the universe” as a whole. If there's some non-isomorphism between properties had by the 'approximation' and properties had by the 'thing' we are approximating, I need more reason than that such a non-isomorphism is possible.
Third, I would like to reiterate the point made in my initial blog post and clarify that Linford does not accurately represent Craig and me in terms of our instrumentalization of the entire GR. We instrumentalize the ontology of spacetime instead. We aren't committing ourselves ontologically to a specific entity 'spacetime'. It is important to note that this perspective does not necessarily align with instrumentalism about GR as a whole, unless one assumes that GR inherently involves a realist view of spacetime, which Craig and I reject. I refer the reader to statements from Craig's books that exemplify this position. For instance, in "The Tenseless Theory of Time" (pg. 122), Craig argues that "a realist interpretation of spacetime actually obscures our physical understanding of nature by substituting geometry for a physical force, thereby impeding progress in connecting gravitational theory to particle physics." This quotation demonstrates that what Craig is instrumentalizing here is not GR itself, but rather spacetime. Similarly, on the preceding page (pg. 121), Craig raises the question of whether the geometrization of gravitation in GR should be understood instrumentally or realistically: "The question raised by the geometrization of gravitation in GR is whether this is to be understood instrumentally or realistically." Thus, it becomes evident that Craig's consideration lies in instrumentalizing spacetime, not GR as a whole. It is adequate to assert that adopting a realist perspective on GR entails a commitment to the reality of a gravitational field. Linford's 'proposal for presentists' (discussed in Linford's section on York Time) is consistent with this: interpreting the General Relativistic metric tensor as a gravitational field superimposed on a fixed Newtonian absolute space and absolute time.
[Even in an attempt at charitability, Linford gets things exactly backward, as far as I can tell. He says: "... instrumentalists could instead say that while we shouldn’t endorse a realistic interpretation of General Relativity, we should adopt a realistic interpretation of a distinct theory of spacetime." But what about the other way around!?: the option of being a GR-realist, but a spacetime instrumentalist!]
At a minimum GR realists need to be committed to the reality of this field. Spacetime realists want this field to be manifested by an underlying spacetime geometry, and so the field itself becomes a four-dimensional, geometric manifold. But that's not how Craig, me, and other spacetime anti-realists conceptualize the relationship between such a field and spacetime geometry. The field doesn't reduce to, or manifest, such geometry realistically construed; it's that the instrumental spacetime geometry is a graphic, visual, mathematical manifestation of the field. On this understanding, the field isn't a four-dimensional, geometric manifold; the spacetime geometry functions as a diagrammatic, visual, graphic depiction of what is, in reality, a three-dimensional hypersurface persisting through time. Since the geometric depiction is dazzlingly beautiful and has amazing heuristic and pedagogical virtues, it becomes an extraordinarily useful tool for making what is mathematically abstract visually concrete. But it seems to have bewitched the imaginations of spacetime realists. They seem to need this depiction to be actually real so that the gravitational field is identified with it, which is an unnecessary jump involving an extravagantly implausible ontology.
[I sharply distinguish this view from views - discussed by Linford in Neo-Lorentzian Relativity and the Beginning of the Universe, 25-26 - that make gμν the gravitational field "defined on a background Minkowski (flat) space-time equipped with a metric ημν", that have the "general relativistic metric" lay "on top of a Minkowski space-time", that there is "an underlying spacetime". Much ado is made about that part of the gravitational field that is "undefined", but these points are made on the assumption that this field is laid on top of Minkowski spacetime, which I deny since I don't think Minkowski spacetime even exists. {Below Linford distinguishes this option from a more presentist-friendly option, which I think is consistent with my views.} The problem here is supposed to be that if spacetime did exist, then every point of this spacetime needs to correlate with a "well-defined value" of the gravitational field. But for singular spacetimes, this field is not defined prior to the singularity, which means that if you lay the field on top of this spacetime, there will be parts of the field that won't have a well-defined value. And if you "truncate" this spacetime to prevent the field from having undefined values, Linford argues that you'd run into skepticism about the age of the universe since such skepticism is the inevitable result of not maximally extending such spacetime. ---------- My view does not lay the field on an underlying spacetime. There is no spacetime. This field is a three-dimensional object persisting through Absolute Time. The view affirms that "the metric gμν appearing in General Relativity" is "a description of space-time", and that the geometric description is intrinsic to GR, but that such a geometry is a manifestation of, or a graphic, diagrammatic depiction of, a real, three-dimensional field persisting through Absolute Time. This view says GR is ultimately a theory about the existence of this gravitational field, which means that if you're committed to this view, you're a realist about GR, even if you're a spacetime antirealist/instrumentalist.]
[Also, let me note a quick correction Linford gave me in the blog: "Damore misdescribes how this is supposed to work, e.g., Damore talks about laying the General Relativistic metric tensor on top of a gravitational field and confuses the Einstein tensor with the metric tensor, but nevermind." --- I agree. I did do this, but if you look at how I wrote it in the blog, it wasn't some devestating conceptual blunder, but a copyist error. I described the tensor mistakenly. I said: "The analogy is that both theories make gμν (Einstein's tensor) describe, not space-time, but some "physical field" "defined on a background space-time." Pitts and Schieve's way of laying gμν on top of Minkowski space-time makes the cosmological singularity infinitely far away. This is because you can't lay gμν on top of a singularity, since there are no space-time points at the singularity, and so if you don't put the cosmological singularity infinitely far away, gμν will end up being laid upon an undefined field." So, I accidentally called gμν 'Einstein's Tensor', when 'Einstein's Tensor' is really Gμν, not gμν. But the point I was making throughout the passage is still intelligible. I use gμν consistently throughout that passage. But I appreciate the point.]
Thus, Linford’s example of Michaela doesn’t fit the position that Craig and I endorse. Craig and I wouldn’t agree with Michaela. Craig and I ontologically commit ourselves to a gravitational field, just as Michaela should ontologically commit herself to the electrodynamic field. Linford explains:
“An instrumentalist might say that while the classical theory is empirically adequate — that is, the classical theory is a tool that can be used to correctly predict the outcomes of experiments — we are not justified in endorsing the claims the classical theory makes about unobservables. Importantly, since we cannot directly observe the electromagnetic field, the instrumentalist would tell us that we ought not endorse the actual existence of the electromagnetic field as part of our ontology. Consequently, for the instrumentalist, endorsing a scientific theory has no direct connection to our metaphysical commitments.”
But Craig and I endorse GR and it does have a direct connection with the existence of the gravitational field. We may understand the relationship between that field and spacetime geometry in a way that denies that the entity spacetime exists.
The realist would offer Michaela different advice. For the realist, if we are committed to a scientific theory, then we are also committed to claims the theory makes about unobservables. (To some extent, this is an oversimplification; typically, realists will claim that we ought to commit to some of the claims that the theory makes about unobservables but perhaps not all such claims.) Thus, realists might tell Michaela that she should welcome the electromagnetic field into her ontology. For realists, endorsing a scientific theory has a direct connection to our metaphysical commitments.
Linford's caveat perfectly accommodates my view: the 'unobservable' that GR commits itself to, in this case, is the gravitational field. And, as even Linford admits, if you have to use spacetime geometry in formulating GR, this doesn't imply that GR realism means spacetime realism. Assuming that GR just is being a realist about spacetime geometry is begging a crucial question from my standpoint, at least.
I need Linford to give me an argument for one of two things: (1) why the spacetime interpretation of GR is superior to all the other physical interpretations, or, what would be more interesting to me, (2) why GR just is being a realist about spacetime (which means making the interpretation/formalism distinction out of place). But then one wonders what Linford meant.
Included in (1) might be some interaction with Craig's reasons for not opting for the spacetime interpretation: that (a) its treatment of "the co-existence relation [...] is implausible", (b) it denies "that things come into being or pass away at all", which "contradicts experience" (Craig later discusses in detail arguments to the contrary from McTaggart, Tooley, Gale, Mellor, and Oaklander), (c) it entails that seemingly 'three-dimensional objects are in reality" "parts of four-dimensional objects" (i.e. perdurantism) (regardless of what has been said about Craig's case against perdurantism failing, the case itself rests on significant laurels, and regardless of the sociological data, the debate about 'persistence' is ongoing), (d) Craig's appeal to Steven Weinberg about it 'obscuring' "our understanding of nature by substituting geometry for a physical gravitational force", which gets in the way of "connecting the theory of gravity to the theory of particles", (e) Craig's argument that "time can exist independently of space (which can be coupled with Craig's discussion of Carlo Rovelli's "What Does Present Days [sic] Physics Tell Us about Time and Space", which discusses "the diversity of the physical time concept", that 'time' as it's used in "spacetime" is a physical time concept, that it's "differently defined in different fields of physics", and that "these operationally defined 'times' are not really time at all but just various measures of time suitable for their respective fields of inquiry") (Craig appeals to Lawrence Sklar and Max Black on this point as well - Craig paraphrases: he advised "scientists to stop talking about 'time' and to refer to their concept simply as 't'", 't' being a "pale abstraction" that "plays a role in physics", and that we shouldn't be "drawing metaphysical conclusions based on" such abstractions), (f) Craig's appeal to Henri Arzeliès, Max Black, and Arthur Fine that most physicists are content to treat, NOT GENERAL RELATIVITY ITSELF, but "the geometrization of gravitation IN GR", instrumentally and not realistically.
(2) seems to be a conceptual identification, so a much stronger justification would be needed. But, first, we've already seen above that Linford already denies such a conceptual identification. And, second, as Craig points out when discussing John Earman's criticisms of Neo-Lorentzianism (how it postulates excessive spacetime structure), all the books that Linford recommends to teach me about Relativity "presuppose a spacetime ontology and therefore cannot be employed to justify a spacetime interpretation of SR over a neo-Lorentzian space and time interpretation." The same can be said for GR.
Fifth, Linford's analogy of the cherry trees in Hume's Dialogues Concerning Natural Religion is (while historically significant!) immaterial for Craig and me. The point being made is that relying solely on observable phenomena to infer the age of the Universe can be limited and may not provide a definitive conclusion. Thus, just as Philo argues that the distribution of cherry trees does not provide conclusive evidence for the Earth's finite age, Linford is suggesting that the distribution of observable phenomena in the Universe, such as the matter-energy distribution, might not necessarily indicate the overall age of the Universe, as opposed to the observable Universe. The problem here is there are significant differences between the two things being compared, so the strength and validity of the analogy weaken for me. Indeed, there is a stark distinction between the "observational evidence" Cleanthes had about the age of the earth based on the distribution of cherry trees, and the observations made in cosmology regarding the observable universe. Yes, both involve observational data, but the sheer scale and precision of the cosmological observations are significantly different and on another level altogether. The observable universe provides valuable information about the overall structure and characteristics of the universe and you can employ statistical methods and models to extrapolate and make inferences about the properties of the universe as a whole based on the observations from the observable universe despite the skeptical catastrophes that Linford seems to be agonizing over. While Linford admits that this is an epistemic worry he has, it looks more to me like a failure of epistemic nerve. This echoes Linford's own sentiments when he says, ". . . this is a kind of skeptical hypothesis no one takes seriously."
Sixth, let's discuss Linford's reasons for thinking his schema can't be satisfied.
FIRST REASON: "When we use the observed matter-energy distribution in order to infer which of the solutions to the Einstein Field Equations best approximates the spacetime that we inhabit, we are only able to make a reliable inference concerning the observable universe. For regions arbitrarily far beyond our cosmological horizon, all bets are off. In fact, there are a set of mathematical results (by Malament, Manchak, Ellis, and others) showing that no matter how well observers in a relativistic spacetime determine the structure of the observable portion of their universe, spacetime as a whole can be almost arbitrarily different. For that reason, supposing that we could infer that the observable universe is finitely old, very little would follow for the Universe."
1. I'm not understanding why we can't extend the approximations given to us by the Field Equations (which apply to the observable spacetime we inhabit), and then extend such approximations to the 'regions arbitrarily far beyond our cosmological horizon'. And it seems to me to depend on what properties of the arbitrarily distant regions we're attempting to approximate. If it's merely the cosmic age component, I'm not so sure that 13.8 billions would be that far off from any possible, unobserved or unobservable regions, and that it's probable that such regions wouldn't be arbitrarily distant.
2. How are the mathematical results from Malament, Manchak, Ellis, and others not just speaking of the mathematical possibilities of 'spacetime as a whole' being different from the structure of the spacetime we observe? I don't deny these possibilities. I'm not sure of anyone that denies them. I'm not sure if Craig would have a problem with these possibilities. None of these possibilities are more likely than any of the other ones. But the probability that the spacetime we inhabit sufficiently approximates the properties of those spacetime regions that lie beyond our cosmological horizon seems to me to be, at least, greater than .5.
3. I couldn't find the Ellis reference in the short bibliography at the bottom of the blog, but I was able to read (to the best of my ability) the papers of Malament and Manchak. Interesting reads, both of them. What I couldn't find is anything that contradicts the main point I'm trying to make, that the multiplication of such observationally indiscernible spacetimes is a modal exercise in logical space that, nonetheless, doesn't seem to move the probabilistic needle one way or the other in terms of it being more or less probable that our observed spacetime region probably approximates those regions beyond our cosmological horizon.
SECOND REASON: "Second, most physicists doubt that singularities are real features of our world. As I’ve said, if we trace the observable universe’s history backwards, according to singular FLRW models, we encounter unboundedly large matter-energy densities and curvatures. To the extent that we should be realists concerning our best physical theories, we ought to think that those theories are approximately true within some domain. But we ought to doubt extrapolations of any scientific theory to domains that are arbitrarily far from the domains in which that theory has been confirmed. I have no idea where the limits of General Relativity’s domain of application might be. But wherever those limits are, we are guaranteed to exceed them if the matter-energy density and curvature can become unboundedly large."
This puzzled me because I've read in Craig over and over again that singularities aren't real features of the world. For example, even in Response to a Video Critiquing the Kalam Cosmological Argument, PART THREE, featuring Linford, Craig says: "The initial cosmological singularity is a mathematical artifact of the standard model. I take it to be an idealization. It's dispensable. Cosmologists often cut out the initial singularity so that the universe, though finite in the past, has no boundary point. Some cosmological models (like the Hartle-Hawking model) round off the initial part of spacetime so that although the past is finite it has no boundary point. Having a beginning does not entail having a boundary point. In any case, the singularity doesn't involve infinite quantities in the Cantorian sense – an actually infinite number of things. As Quentin Smith points out, it's really a case of division by zero. You have the mass of the universe over zero volume which yields infinite density." I'll let that stand as emblematic of Craig's position rather than multiply quotations. So, what's Linford's point? It's the idea that if matter-energy densities and curvatures become infinitely large, we are likely to exceed the boundaries of GR's applicability, suggesting that we should be cautious about drawing conclusions about the entire universe based on extrapolations involving singularities. But this leads to another point about how to interpret the scope of GR's applicability.
There are two places (off the top of my head) where we get a hint at how Craig interprets GR's scope.
First, as I mentioned in my first blog (and which I'm anxious to know what Linford makes of this), there were lecture notes handed out by Craig himself to a class at Houston Baptist University (the name of the institution at the time) on KCA. I've since seen chunks of these notes reproduced on his ReasonableFaith website entitled Big Bang Cosmology. In this link, I'm specifically referring to Craig's comments in footnote 7, which provides extra commentary on his point that, "If there is such a non-classical region, then it is not past eternal in the classical sense. But neither does it seem to exist literally timelessly, akin to the way in which philosophers consider abstract objects to be timeless or theologians take God to be timeless. For it is supposed to have existed before the classical era, and the classical era is supposed to have emerged from it, which seems to posit a temporal relation between the quantum gravity era and the classical era."
(**Notice that Craig agrees with me that the non-classical region doesn't exist timelessly the way God does, corroborating what I said above against Linford's point that if the spatiotemporal universe emerged from some non-spatiotemporal state, then the universe could have an initial temporal state [a first temporal state] and not begin to exist. If the universe emerged [a temporal concept, so far as I can see] from this state, and the state isn't timeless as God is, then this undercuts Linford's analogy between God and this non-spatiotemporal state of the universe as it pertains to having a first temporal state and beginning or not beginning to exist simultaneous with this state. But I digress.)
Let's look at footnote 7 one thought at a time to be precise.
"Christopher Isham observes that although quantum cosmogonies 'differ in their details they all agree on the idea that space and time emerge in some way from a purely quantum-mechanical region which can be described in some respects as if it were a classical, imaginary-time four-space” (C. Isham, “Quantum Theories of the Creation of the Universe,” in Quantum Cosmology and the Laws of Nature, second ed., ed. Robert Russell et al. [Vatican City State: Vatican Observatory, 1996], 75)."
What Isham seems to be hinting at is the idea that the quantum-mechanical region can be described in some respects either quantum-mechanically or classically ('the classical, imaginary-time four-space'). Now, this 'four-space' seems like something that is within GR's scope, and so GR can describe this quantum-mechanical (or 'non-classical') region (or regime) in the relevant respects, presumably, the classical respects.
But moving on to the tension between spacetime emerging diachronically or synchronically, Craig comments: "This feature of quantum cosmogony is very problematic, since diachronic emergence of time is obviously incoherent. But how can one make sense of a synchronic emergence of time as a supervenient reality in the context of cosmogony? The most sensible thing to say seems to be that the Euclidian description is a lower-level description of classical spacetime prior to the Planck time. So the same reality is being described at two levels."
So, Craig is dividing spacetime reality into (1) a non-classical, quantum-mechanical region prior to Planck time and (2) Planck time onward. Thus, prior to Planck time, we can give two descriptions of that non-classical region: a 'Euclidian' one (which is classical) and a quantum-mechanical one (non-classical). Craig calls the Euclidian description a lower-level description, meaning that it's not as precise or fine-grained, or powerful enough to capture the quantum-mechanical phenomena operating on a higher level. It is, therefore, outside the scope of GR to describe these quantum phenomena on that level. However, the last sentence of the above quotation is absolutely crucial and needs to be addressed: the SAME REALITY is described at two levels.
What does this imply? Craig tells us: "That implies that if the classical spacetime has a beginning, then so does the quantum gravity regime. For they are descriptions of the same reality. In the one a singularity is part of the description; in the other it is not. So what is prior to the Planck time is not the quantum gravity era as such; rather what is prior is the classical period of which the quantum gravity description is the more fundamental description."
What Craig is doing is here correcting the way this is usually graphically represented. Consider the following image:
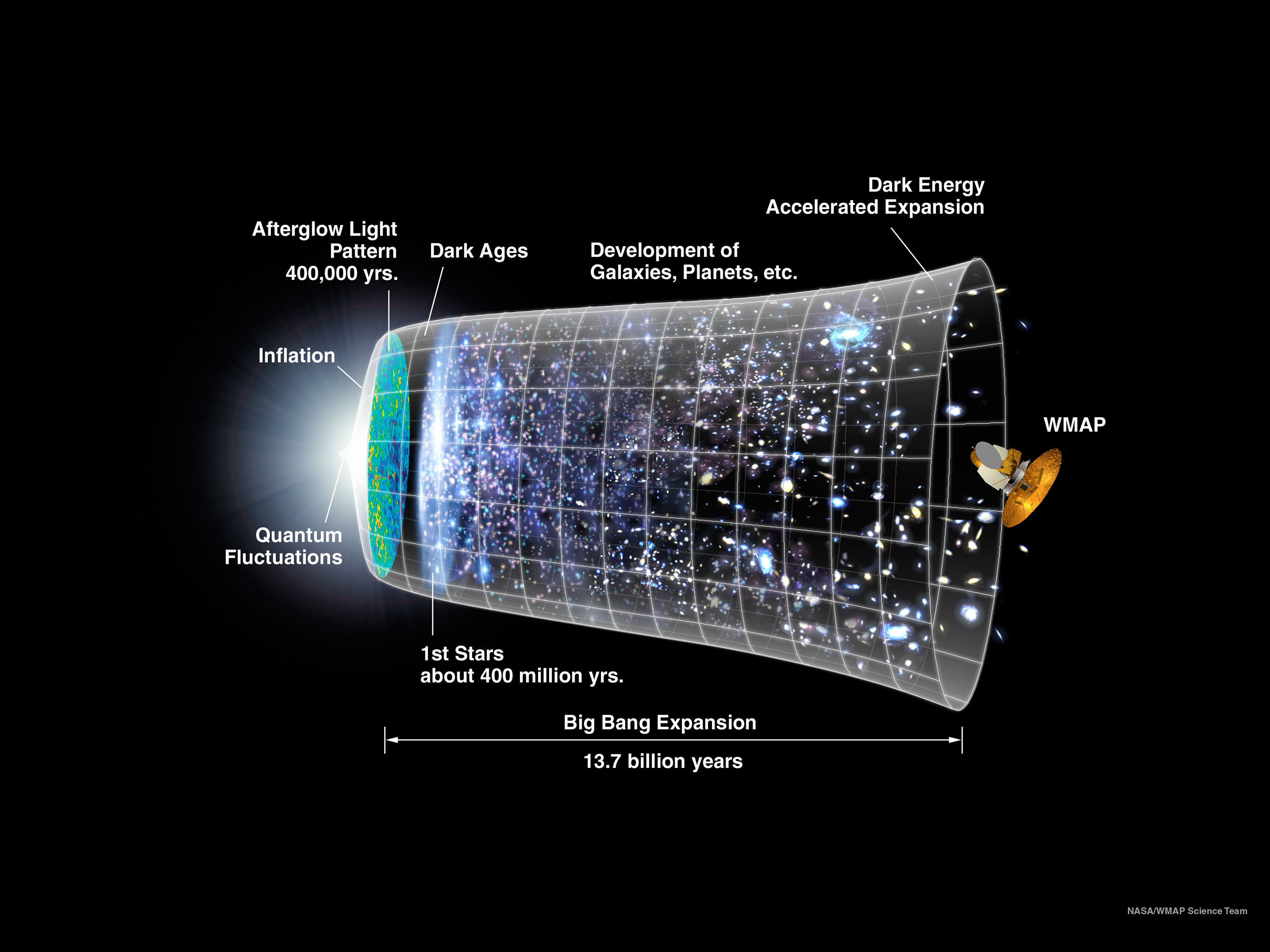
See the bright point labeled 'Quantum Fluctuations', which is at the very, very starting point of the graphic representation? It's represented as before everything else on the graph. While this may help pedagogically, Craig is suggesting that this may not be strictly accurate. There shouldn't be a 'bright point' prior to 'everything else', where the bright point is the quantum regime and everything else is the classical regime. There should be one graphic representation of which the classical description applies to the whole thing, including the bright point, but also a quantum-mechanical description that applies to the bright point, which is more fundamental than the classical description. There is a parallel here to Donald Davidson's Anomalous Monism in the Philosophy of Mind, where the mental and the physical are not ontologically distinct (monism), but this monism can be given mental and physical descriptions, and depending on what is being described, either the mental or the physical description may be the more fundamental description.
Craig goes on: "If this is correct, then, given the beginning of the classically described universe, it is impossible for the universe as quantum gravitationally described to be without a beginning. For they just are the same universe at different levels of description."
To me the inference is obvious. The scope of GR, cosmologically applied, encompasses classical descriptions that have ontological ramifications for the universe as quantum gravitationally described. Recall what Linford's worry was: "I have no idea where the limits of General Relativity’s domain of application might be. But wherever those limits are, we are guaranteed to exceed them if the matter-energy density and curvature can become unboundedly large." Even if the boundaries between GR's domain of application and beyond are fuzzy, why can't we conceive of this domain in terms of the properties circumscribed by these descriptions? When the matter-energy density and curvature become unboundedly large, the quantum-mechanical description becomes, at some point, the more fundamental description. GR can still describe this domain, but it won't be precise enough to account for the domain's quantum mechanical properties.
In summary, Craig's viewpoint is that GR's scope is encompassed by both classical and quantum descriptions of the universe. While GR might not provide a fully detailed account of the quantum regime, it still has ontological ramifications for that regime. The relationship between classical and quantum descriptions involves different levels of granularity and precision, with the quantum description being more fundamental for the initial stages of the universe.
The second place Craig talks about the scope of GR is mentioned by Linford, but it's not interacted with (at least in the present paper). It's in On Non-Singular Spacetimes and the Beginning of the Universe, by Craig and James Sinclair. It's worth quoting the entire thing:
"Isaac Asimov, in an article entitled “The Relativity of Wrong” [Asimov, 1989], pointed out the fallacy of believing that current “primitive” models lack usefulness because they are “wrong,” given that a future theory is always just over the horizon to overturn the current one. There are degrees of “wrongness,” and theories which are less wrong than their predecessors are so because they take account of what is empirically correct in their forebears. It is simply mistaken to think that phenomena predicted and analyzed by GTR (especially indirectly observable phenomena such as black holes) via such things as singularity theorems cease to be relevant because a different mathematical formalism may someday come into general use. There may be no such things as singularities, per se, in a future quantum gravity formalism, but the phenomena that GTR incompletely strives to describe must nonetheless be handled by the refined formalism, if that formalism has the ambition of describing our universe. This can be seen in the above example of the Wheeler-Dewitt approach as described by Kiefer. Big Bang Friedmann universes with a meaningful time coordinate are recoverable in the theory (as Kiefer shows) but are described as a semi-classical WKB approximation which invokes a mechanism called decoherence. They, in fact, must be recoverable because that is what we see. If Big Bang Friedmann-like behavior were not recoverable, that in itself would be grounds for rejecting the larger theory."
The underlined portion is what Linford quotes in his seminal paper. This portion is in the context of Isaac Asimov's argument against dismissing current scientific models as completely "wrong" because they are expected to be replaced by future theories, that there are degrees of "wrongness" in scientific models, and newer theories build upon the empirical correctness of their predecessors. The relevance of phenomena predicted and analyzed by GR, including black holes, should not be undermined simply because a future mathematical formalism might supersede GR. In particular, while a future quantum gravity formalism may eliminate the concept of singularities, it would still need to account for the phenomena that GR aims to describe. In the example of the Wheeler-DeWitt approach mentioned, Kiefer demonstrates that Big Bang Friedmann universes with a meaningful time coordinate can be recovered within the theory using a semi-classical WKB approximation and decoherence, and the recovery of such behavior is essential because it aligns with our observations. If the larger theory did not allow for the recovery of Big Bang Friedmann-like behavior, it would raise concerns and potentially lead to the rejection of the theory.
I'm told something along these lines all the time when it comes to Newton's theory of gravity, which is incredibly successful in explaining the motion of objects on Earth and many celestial phenomena, and despite being superseded by GR, Newtonian mechanics still retains significant applicability in many domains of everyday life and engineering. The analogy is that GR shouldn't (and doesn't) dismiss or ignore the phenomena that Newtonian mechanics successfully explains within its domain of applicability. While GR provides a more comprehensive and accurate description of gravity in the presence of strong gravitational fields and high speeds, it should still account for and be consistent with the well-established results of Newtonian mechanics in situations where its effects are negligible. Therefore, GR must be able to reproduce the predictions of Newtonian mechanics in the appropriate limit, such as when speeds are much smaller than the speed of light or when gravitational fields are weak. By doing so, GR can demonstrate its consistency with well-established empirical observations and provide a smooth transition from Newtonian physics to the more comprehensive framework of GR.
In the same way, when/if a future quantum gravity formalism eliminates the concept of singularities, it would still need to account for the phenomena that GR aims to describe. So, in the example of the Wheeler-DeWitt approach (above), Kiefer demonstrates that Big Bang Friedmann universes with a meaningful time coordinate can be recovered within the theory using a semi-classical WKB approximation and decoherence, and the recovery of such behavior is essential because it aligns with our observations. If the larger theory did not allow for the recovery of Big Bang Friedmann-like behavior, it would raise concerns and potentially lead to the rejection of the theory.
Unfortunately, all Linford says in response is: "I don’t find this reply convincing. However, whether or not we should look upon divergences in physical theories as suspicious has been discussed at length elsewhere and I set the issue aside for the purposes of this paper."
There's a little more elaboration in Linford's footnote 14 (in the seminal paper): "While the predictions of a theory within a specific domain may provide some inductive evidence that the theory will apply to neighboring domains, no one should have confidence that the theory will apply to domains that are arbitrarily distant. Consider approaching a point p where the energy density diverges. As one approaches p, one encounters arbitrarily large energy densities and so one inevitably encounters energy densities which surpass the domain of applicability of General Relativity before one reaches p. For that reason, ceteris paribus, we should doubt the predictions made by General Relativity within the vicinity of curvature singularities."
But Craig's approach, so far as I can see, allows for the accommodation of this worry: it recognizes that the classical description within GR represents a higher-level approximation and that a more fundamental quantum description may be necessary for these other extreme domains. By incorporating two levels of description, Craig acknowledges that the classical description of GR has limitations and that a more refined and fundamental theory may be required to fully understand the physics near curvature singularities, which perfectly aligns with the ongoing quest to develop a theory of quantum gravity that can reconcile the principles of quantum mechanics and general relativity.
I see Craig's strategy as a conceptual framework or parameter for addressing the worry about the applicability of GR near curvature singularities, and that, of course, the specific details and formulation of a theory of quantum gravity are still open questions in the field of theoretical physics. When a new theory, like a theory of quantum gravity, supersedes GR, it is expected to provide a more complete and accurate description of the underlying physics. But to maintain continuity and consistency with the successes of GR, this new theory must also be able to account for and explain the phenomena that were correctly accounted for by GR within its domain of applicability, ensuring that the new theory builds upon the empirical successes of the earlier theory and provides a seamless transition between the two frameworks.
In the case of Craig's strategy of involving two levels of description, the classical description within General Relativity (GR) represents the earlier theory that has been successful in explaining various phenomena related to gravity, space, and time. But as physics advances, it is anticipated that a more fundamental theory, such as a theory of quantum gravity, will supersede GR, providing a more complete and accurate description of the underlying physics.
But the takeaway here for me is that this strategy supports the point that, given the beginning of the classically described universe, it is impossible for the universe as quantum gravitationally described to be without a beginning. The classical description within GR and the quantum description are both descriptions of the same underlying reality at different levels of granularity and precision. These two descriptions refer to the same universe, and so if the classical description has a beginning, the same must be true for the quantum gravity regime. Thus, the two descriptions are intertwined and interconnected, and any theory that aspires to describe our universe comprehensively must address the notion of a beginning.
So, I fail to see how Linford's second reason undermines the satisfaction of his schema.
THIRD REASON: "Third, we have strong independent reasons to think that General Relativity cannot be extended to arbitrarily large matter-energy densities. General Relativity is not compatible with quantum field theory; thus, we ought to expect that General Relativity will be replaced with some successor theory. There are good reasons to expect that the successor theory will describe what happens when the matter-energy density is sufficiently high. Without such a theory, we simply do not know what happened in our universe around the time of the Big Bang."
I've dealt with this above. Of course, Craig would acknowledge that there are indeed strong reasons to expect that GR will need to be extended or replaced with a successor theory, especially when it comes to incorporating quantum field theory and addressing extremely high matter-energy densities. And he would agree that the limitations of GR imply the necessity of a more comprehensive theory that can describe the behavior of matter and energy in those extreme conditions. But Linford is wrong (again, as far as I can see) to think that we are completely in the dark here. The classical description within GR, despite its limitations, still provides valuable insights and empirical predictions that have been confirmed by observation and experimentation.
As I did above, when you invoke Craig's conceptual strategy of two levels of description, all you have to show is that while the classical description may not capture the full quantum nature of the universe in those extreme regimes, it's still a valid and useful higher-level approximation that has been awesomely successful in the relevant domains, providing a foundation from which future theories can build upon and refine.
Then, just couple this strategy with the idea that the classical and quantum descriptions are different levels of description of the same underlying reality. So, if the classical description of GR includes a beginning, then the same must hold true for the quantum gravitationally described universe. Both descriptions refer to the same universe but at different levels of granularity and precision. So, "the phenomena that GTR incompletely strives to describe must nonetheless be handled by the refined formalism, if that formalism has the ambition of describing our universe.", the phenomena being the behavior of matter, energy, space, and time near curvature singularities (such as those predicted in the early stages of the universe or in the vicinity of black holes), and perhaps a potential non-singular beginning; the refinement of the GR formalism, such as a future theory of quantum gravity, would aim to provide a more comprehensive understanding of that phenomena.
Therefore, nothing that Linford has presented has given me a reason to doubt that his schema can be satisfied by what Craig has offered.
----------------------------------
3. Linford's Section On The Problem of York Time
3.1. I'm going to skip Linford's remarks about spacetime solipsism, framentalism, and Linford's take on Craig's view (Relativity being empirically adequate, but not literally true) and begin this section with a priming of the pump of my own. I begin with a time-stamp of a YouTube video of Craig at Baylor talking about the relationship between metric time and the Kalam and go to 38:23. Here are the transcripts:
"You are correct in saying that technically the Kalam cosmological argument doesn't really prove the beginning of time. What it proves is the beginning of metric time: that there cannot be an actually infinite number of arbitrary but equal nonzero finite intervals regressing into the past. And so the question arises: before clocks existed, before we had the expanding universe, did God literally exist before the universe in a nom-metric time? And the Kalam argument is consistent with that hypothesis. If you are persuaded that, as you put it in one of your books, at the first moment of time, it was true that there were swans or there were not swans prior to this moment, that implies there was a prior moment at which God existed. And this argument is consistent with that. I myself would disagree with you and Lukas [sic] and Alan pageant [sic] on your . . . [interruption] I give arguments against the metric conventionalism that I think you and Lucas and Padgett presuppose for your view. So, while your view is I think a legitimate and compatible option with what I've shared in the end, I opted for God being simply timeless sans the universe..."
You can nuance this even more with Craig's discussion of Alan Padgett's appropriation of Rudolph Carnap's rules for the metrication of time: addivity, equality/congruence, and the unit rule. It's not important for my purposes to explain what these rules are. I mention it to highlight a contrast Craig is making between two different metrics. Craig explains that Carnap's rules involve, "... laying down conditions for physical, metric time, not simply metric time, as Padgett assumes." Thus, there is (1) a physical, metric time and (2) a 'simply metric time'. Craig dovetails this distinction onto Newton's distinction between metaphysical and measured (clock or any metric based on 'natural periodic processes') time: "For Newton, metaphysical time, God's time, possesses an intrinsic metrication and therefore is not dependent for its metric upon a standard clock or a natural periodic process." Craig will disagree with Padgett that if God is not in or related to this physical, metric time, then God is not in any time at all. God may still be in a metaphysical time with its own intrinsic metrication, as Craig cites Kroes as explaining:
"To Newton it was self-evident that there exists just one fundamental metric for time: the intrinsic metric of absolute time. Physical processes of whatever kind could provide a more or less accurate 'sensible measure' thereof. A 'true' sensible measure of absolute time could only be reached in the case of a perfectly isolated, completely undisturbed periodical system which would constitute an ideal clock. In a certain sense, all physical processes had to obey, according to Newton, the rhythm of absolute time; an ideal dock, of whatever nature (mechanical, gravitational, etc.) could provide an exact measure o f the unique, fundamental metric of absolute time."
This intrinsic metric of absolute time is just another name for the intrinsic metric of metaphysical time, Craig's famous example being Henri Poincare's "une intelligence infinie", a role God could conceivably assume. God would then be in the relevant metaphysical position to "...classify events as past, present, or future according to His time.", which would mean that "...God's present is constitutive of relations of absolute simultaneity." God's present would then constitute a privileged reference frame, implying some kind of Neo-Lorentzian take on Special Relativity (where we'd have a hyper-plane of simultaneity constituting a single, privileged inertial frame); and then when it comes to General Relativity, such present events are constituted by the relevant inertial frame and a geometrically represented, three-dimensional hyper-surface of spacetime.
Let's list the relevant concepts we can use here:
1. Absolute/metaphysical time
2. Physical/measured time
3. The idea that physical time can measure metaphysical time accurately as an approximation when in uniform motion relative to the reference frame of metaphysical time.
4. When physical time deviates from metaphysical time, that means it is not in uniform motion relative to metaphysical time and we have time dilation.
All of this Linford is aware of and reiterates in his paper and his blog response. What I find puzzling are the inferences he seems to draw from this. For example, Linford argues:
"If we follow the Neo-Lorentzian strategy, what happens to the inference that U has a finite age? On the Neo-Lorentzian strategy, there are two different ways that we can talk about time. On one hand, there is time as measured by physical clocks; let’s call this parameter physical time. Physical time is the time used in one standard expression of the General Relativistic metric tensor and not the time associated with the underlying Newtonian absolute time. And since physical time is merely an apparent time, without any underlying metaphysical reality, whether physical time is finite to the past has no direct relevance for the KCA. Whether U is finitely old — in the sense that does have relevance for the KCA — should be understood as a question about whether U has finite age with respect to the underlying Newtonian absolute time."
Now, before we launch right into Linford's discussion of York Time as a rival to Cosmic Time as a candidate for 'Absolute Time' (the relationship Linford poses between these categories I'm already having trouble with), I find the above paragraph conceptually disorienting.
First, why is physical time merely an apparent time, without any underlying metaphysical reality? How could this be in all the relevant contexts? If a clock is in uniform motion relative to a privileged reference frame, and that privileged reference frame sufficiently approximates/measures God's metaphysical time (Newton's Absolute Time), then how would that clock (this particular physical measure) not have an underlying metaphysical reality?
Second, if such a clock (such a 'parameter time') is in such uniform motion, how could such a physical time not have direct relevance for the KCA? Remember what Craig said above: "...technically the Kalam cosmological argument doesn't really prove the beginning of time. What it proves is the beginning of metric time..." What else could this 'metric time' be but the particular measures metrically carved out by the variety of readings a clock could denominate for us: minutes, hours, years, centuries, days, etc.? Doesn't this mean that the beginning of this Cosmic metric doesn't necessarily correlate with the beginning of Absolute/Metaphysical time? U being finitely old relative to this Cosmic metric is entirely relevant to the KCA. That the finitely old Cosmic metric doesn't have a direct correspondence with the beginning of the intrinsic metric of Absolute/Metaphysical time is completely irrelevant to me.
What I think Linford should be saying here is that the Cosmic metric has to be in uniform motion relative to the intrinsic metric of Absolute Time. The purpose of this isn't to align the two metrics in terms of their beginnings but to ensure that the Cosmic metric is privileged. If the Cosmic metric is constituted by such a privileged reference frame, then showing that the Cosmic metric has a finite beginning entails showing U's finite beginning, regardless of whether or not U's finite beginning aligns with the intrinsic metric of the beginning of Absolute Time.
Linford adds: "Craig and company are not alone in adding absolute time to relativistic physics. Although the view that there is an absolute time is not popular among physicists, some physicists have seriously defended absolute time. For example, Roser and Valentini have defended the view that a parameter called York time should be understood as absolute time. (For citations of Roser and Valentini’s work, see my original publication.)"
But I can't find anywhere in the literature from Craig, or anyone else, of anyone adding Absolute Time to physics. Yes, Absolute Time will be part of the biggest metaphysical picture of what is going on in terms of including in the scope of one's largest descriptions of all aspects of reality, physical and metaphysical. But Relativistic Physics will always be part of the physical description, and this physical description will, in part, describe (approximate to) Cosmic Time, understood as a parameter. As Craig explained above, this is all we need for circumscribing the requisite approximation to Absolute Time, an approximation that's more the purview of the philosopher of time or the philosopher of physics, not theoretical physicists with their ts and Ts. Even Philipp Roser and Antony Valentini (in Cosmological history in York time: inflation and perturbations, cited by Linford) talk about a fundamental time parameter (York Time), not Absolute Time. Sure, it may or may not be tied to the relevant context that Craig's Newtonian project is concerned with, but nothing in the paper explicitly tethers their points to such metaphysical animadversions. My charitable explanation is that labels are being used here equivocally. This is unwitting, of course, since Linford, along with the academics Linford has read, may be using nomenclature in a way that doesn't perfectly align with the way Craig is using it. But it's our job when doing syntopical analysis to make the unwitting equivocation explicit in our 'agony of verbal precision' (Chesterton, I think) (and for more on 'syntopical reading' go to Adler's How to Read a Book).
3.2 Time and the CMC Foliation
With this prolegomenon on metrics sufficiently finetuned, let's turn to the first extremely important issue of Time's relationship to the Constant Mean (Extrinsic) Curvature, a.k.a. the CMC foliation. Clarifying exactly what this foliation is and how it relates to York Time and Cosmic Time is the first step in understanding why the York Time labeling is dialectically harmless when it comes to the KCA generally, and as a meaningful rival to the Cosmic Time labeling. One of my main theses is that Linford isn't understanding York Time completely in this domain. Either that, or I'm not, and I'm open to correction here. Nevertheless, I've spent the better part of 4 months researching York Time and I can't see it in any other light.
Spacetime is represented in both Special and General Relativity as a four dimensional block. (Note that I said “represented as”. The former sentence should not be read as a metaphysical commitment to four-dimensionalism.) We can “cut” that four-dimensional block into three dimensional slices in various ways; any given cutting of the four dimensional block is called a foliation. Advocates of absolute time think that there is a single best foliation, where each three dimensional slice corresponds to a moment of absolute time. And there are various theoretical reasons to think that a particularly good candidate is a slicing into hypersurfaces of Constant Mean (extrinsic) Curvature, that is, what’s been called a CMC foliation. (For a non-technical introduction to the CMC foliation, see Laycock 2005, pp. 118-121.
Of particular interest to me is this idea of slicing. Linford accidentally cites Michael Lockwood as 'M. Laycock' in the blog, but the book Linford cites is The Labyrinth of Time: Introducing the Universe for the 'non-technical introduction'. He asks us to start on pg. 118, but I'll start back on pg. 115 at a section called God's Foliation. As I read through Lockwood's section here, nearly everything Craig has said about Cosmic Time finds confirmation. The only difference I see initially is Lockwood's decision to call Cosmic Time a time coordinate, rather than a time parameter. But there are places where Craig temporarily does the same thing, but then goes the extra mile by making that coordinate a parameter because of its being privileged in the way it is.
Lockwood cites Sir Michael Berry as demurring on this point, but he seems to me to make the same mistake in the nomenclature I noted above. Berry thinks Cosmic Time just is Absolute Time. No, with Newton's distinction between Time and its measures, acknowledged by Linford, Cosmic Time is supposed to be a measure, or a metrical approximation to, Absolute Time, not Absolute Time itself. This conflation happens over and over again in my reading.
Lockwood informs us of the importance of the CMC foliation in 'defining' Cosmic Time, but Lockwood brings up the point that if "... we assume, for the sake of argument, that such a foliation is available in the real universe (something that we shall be questioning in later chapters), a critic of this approach could still argue that, given the foliation-invariance of general relativity, there is scant reason to ascribe a unique metaphysical significance to this way of foliating space–time." This doesn't do anything for me because it doesn't interact with what Craig has said as to why he thinks such a foliation is available in the real universe (when GR isn't considered in abstracto, and thus with a 'foliation-invariance'). All we have here is this promissory note (a discussion he will have in 'later chapters') and James York's proposal for cosmic time. How convenient!
[Sidebar: At one point, Linford corrects me, writing: "At one point, Damore claims that the hypersurfaces in an FLRW spacetime should be understood as hyperplanes: “From what I understand, that particular kind of ‘slicing’ is why some call this a ‘hypersurface’, even if, mathematically speaking, it’s a hyperplane.” This is confused in two ways. First, a hyperplane is a kind of hypersurface. Second, the CMC hypersurfaces are not generally flat, even if we make the restriction to FLRW spacetimes and even if we say that only one (“present”) hypersurface is actual.)" This confuses me for two reasons. First, if a hyperplane is a kind of hypersurface, then I'm not sure how what I said was in need of correction at all, namely, that, mathematically speaking, hypersurfaces are hyperplanes, those hypersurfaces that are a kind of hyperplane, obviously. I wrote that while aware that hyperplanes are generally flat, while hypersurfaces are generally curved. Yet Linford submits that hyperplanes are a kind of hypersurface, which is synonymous with what I had written. Second, if CMC hypersurfaces are generally curved, of course, the actual hypersurface will be curved as well. How did what I said imply anything contrary to this?]
Linford: "If friends of absolute time want to tell us that the hypersurfaces in the CMC foliation correspond to moments of absolute time, they will need to provide us with a procedure for selecting which CMC foliation is the correct one. But let’s set that issue to one side. Let’s suppose that we either have such a procedure or that we are considering a spacetime model in which the CMC foliation is unique, such as a closed FLRW model. Once we have the desired foliation, we need to label the hypersurfaces in the foliation with a time parameter."
This lays the groundwork. The issue Linford is setting to one side will come up later. Craig does have a case for selecting the correct CMC foliation (I'll bring up details as needed below), but Linford's complaint will be that such a case isn't sufficiently exclusive for keeping York Time at bay (isn't "unique", as Linford says). And since Craig's case for selecting the correct CMC foliation is within the context of a closed FLRW universe, the direction that Linford is taking is copasetic for my purposes.
Linford: ". . . the aforementioned labeling of the hypersurfaces in the CMC foliation is not unique. There are an infinite number of ways we can label the hypersurfaces in one and the same CMC foliation and each of those labelings are possible candidates for the absolute time. One candidate that enjoys many of the same advantages as cosmic time is the York time, that is, the value of the average extrinsic curvature itself; moreover, as I will explain below, some would argue that the York time is a better candidate for absolute time. I do not endorse absolute time myself and I am currently undecided on whether York time actually is the superior candidate. Instead, my argument is that, insofar as I can tell, there is no particularly strong reason why proponents of absolute time ought to favor cosmic time nor have they provided an adequate response to arguments for the view that York time is the superior candidate. Without having adequately ruled out York time, they haven’t succeeded in mounting a scientific case for the KCA’s second premise."
Neither Craig nor I (nor anyone I've read) denies that there "is an infinite number of ways we can label the hypersurfaces in one and the same CMC foliation and each of those labelings are possible candidates for absolute time." This is reminiscent of the similar point made above about GR considered in abstracto. What's relevant for Craig's purposes is picking a labeling of this CMC foliation that is de facto connected to the distribution of the universe's matter/energy, a distribution that traces the overall expansion of the cosmological fluid in such a way that the cosmic singularity (if we're talking about singular models) is approximately 13.8 billion years ago, not removed to past-infinity as York Time has it. If this labeling is so connected, then the relevant hypersurfaces that are labeled in this way are the relevant hypersurfaces for approximating absolute time.
Now, we're getting to York Time. I will get into the relevant details as Linford brings them up. I do this, rather than provide a lengthy compare/contrast mini-essay on Cosmic vs. York Time so that the reader can see exactly where the points of contention are located. As I foreground these points of contention, my interaction with Linford and Roser will come out, along with my interpretations of their work, and therefore my conclusions about why York and Cosmic time aren't rivals at a particular level of description. If they're not rivals in the relevant sense, then, contrary to Linford, neither Craig nor I need to rule out York Time in mounting a case for the KCA's second premise. I will make this perspective more clear below. But before I do, let me quote Linford here to get to the crux of the issue as to why he thinks they are rivals:
Consider one of the singular FLRW models and let’s suppose that we’ve identified one of the CMC foliations as the one that correctly cuts the model into moments of absolute time. While the cosmic time might tell us that the singularity is finitely far into the past, so that the Universe, so depicted, is finitely old, the York time labels the singularity as infinitely far into the past. So, unless we have a reason that adequately breaks the symmetry between cosmic time and York time as candidates for measures of absolute time, we cannot tell whether, according to absolute time, the Universe has a finite or infinite age. Thus, we cannot tell whether the Universe began to exist.
As I hope to explain below, based on my close reading of James York and Phillip Roser, when it is said that York Time labels the singularity as infinitely far into the past, there is a certain sense attached to this that is consistent with the universe being 13.8 billion years old. Actually, allow me to go into this a little here. Let's start with Cosmological history in York time: inflation and perturbations (2017, Philipp Roser and Antony Valentini). The relevant passage is in section V (Re-entry in the Radiation-Dominated Era). If the previous sections are contextually relevant, I'll bring up those details where needed. I specifically want to draw attention to footnote 9, which has the relevant wording:
9 Any explicit relationship between t and T can be modified by translation in t since the cosmological equations in t are time-translation invariant. However, the York-time theory is not T-translation invariant since T has a physical meaning and the equations are explicitly T-dependent. The relationship given here therefore depends on the appropriate choice of time origin, namely that t = 0 corresponds to T = −∞.
The context here is the radiation-dominated era following the inflationary period, discussing the concept of 'reheating' and the way the universe transitions into this particular phase. (You also get details about how the scale factor and the Hubble radius evolve and how those allow for 'frozen' modes to 're-enter' and evolve.) But the relevant point for me is that, in this context, both t (cosmic time) and T (York Time) seem to me to be serving as different ways to parametrize the evolution of the universe. So, the relationship between t and T (in the radiation-dominated era) is supposed to be described as T = −M2P l/t (I wish I knew how to annotate the super/sub scripts properly, but I can't right now. The '2' is squaring -M and P l is a subscript to -M. That quantity is then divided by t.) Thus, as t APPROACHES ZERO, T approaches negative infinity: T→−∞.
This is what I make of this so far. Roughly, t = 0 is the theoretical Big Bang, which makes t cosmic time; Roser/Valentini call it cosmological time. T, of course, is York time, a different parametrization of time. What this seems to mean is that AT t = 0, roughly 13.8 billion years ago, at that particular time, T = −∞. So, T is REPARAMETRIZING a finite interval. It's "stretching" the beginning of the universe to negative infinity, providing a different mathematical description of the singular initial conditions of the Big Bang that, at a cosmically temporal level of description, happened roughly 13.8 billion years ago. Specifically, with T, it's the PLANCK ERA that 'stretches' (T = −∞) just prior to the commencement of inflation. Thus, York time is being offered as a more 'natural' way to describe the EARLY UNIVERSE, prior to inflation, to avoid extremely small time values that Cosmic time has problems describing (like the Planck era). It's a mathematical re-framing of cosmic history.
Roser/Valentini continue: "The York time description clearly does not do away with absurdly large order-of-magnitude differences in the way Misner might have envisioned. Rather, periods of large T-duration are of short t-duration and vice versa. The infinite ‘York age’ of the universe might however be considered an aesthetic advantage."
So, what does this mean? It seems to imply that what appears to be a very long period when measured using York time could actually pass quite quickly when measured using the standard cosmological time t. Okay. What's going on here? Let's apply this cosmologically to our universe. For example, the very early moments of the universe, close to the Big Bang, might be described as happening in a minuscule sliver of cosmic time (t), yet they could occupy a vast duration when measured in York time (T). So, T is offering a different perspective on the sequence and duration of cosmic events, which has implications for understanding the underlying physics, of course. So, for example, if a certain cosmological event spans a large range of York time T, it might actually take place in a very small interval of t. The reverse is also true: events that are quick in York time might be drawn out in cosmic time.
So, how in the world is T relevant for understanding or undermining premise 2 of KCA? All T would be doing in this context is reparametrizing what t would be parametrizing if t's A-theoretic sense had been relevantly substituted by T's A-theoretic sense (when interpreting 'began to exist' when applied to 'the universe'). In other words, the negative infinity characteristic of T (York time) is perfectly compatible when describing a 'finite interval' of cosmic time t (a 13.8 billion-year-long temporal interval). So, there seems to me to be a subtle equivocation going on here. Linford wants/needs this 'negative infinity' to mean 'past eternal' and he wants/needs 'past eternal' to have the sense it would have if cosmic time t were said to be past eternal (where instead of t signifying 13.8 billion years, it would signify an actually infinite number of years). But that's just not what's going on here.
This interpretation is further corroborated when Roser/Valentini talk of cosmological eschatology: T = 0. How do we describe the universe ceasing to exist at some future time (say, in a Big Crunch): "One might speculate whether York time really ‘ends’ at T = 0 or whether cosmic history continues and our description ought to be extended. Indeed, if T does have fundamental physical significance, then it is unwarranted to conclude that the universe would end then simply because the usual parameter t ceases to describe such speculative future eras, although problems may arise if physical quantities are not well behaved during the transition to T > 0." Okay, but why would t cease to describe such future eras? What is it about these 'eras' that make t unable to describe them? Nothing here indicates that such an era is 2 years, or 10 minutes, or 1,236,934 seconds, or 75 hours, or 13 centries, or a couple thousand millennia past the era that t can describe. In terms of t, when does it happen that t ceases to describe the eras it can describe? What is significant about that 'transition'? And when it comes to T, what would '>' even mean here if we can't bring up any cosmic matrices? Roser's dissertation has a section that helps a little: Transition behaviour and classification of potentials. First, in Figure 6.1, Roser notes 'corresponding values' between T and t, where t = 0 corresponds to T → ∞, which further bolsters my case that the kind of infinity involved in T → ∞ has nothing to do with the kind of infinity involved in KCA's second premise. Roser argues that the 'finite starting value of t' is ". . . up to convention (due to cosmological-time translation invariance)", but what does that mean? Does it mean that the finitude of the value is conventional or that the finitude of the value is conventional? Is the translation invariance referring to the translation of t and T or is it referring to the different values of t? Since Roser is referring to "The finite ‘starting’ and ‘end’ values of t and t′", I'm assuming that he's referring to the invariance to values of t. Okay, but then the past-finitude of the universe isn't conventional; it's the value of t that parametrizes that past-finite interval that is conventional (as long as the intervals are equal, finite, arbitrary, and non-zero, as Craig has specified).
So far, all that's going on here is that T is being preferred to t because T (and not t) is what's more successful in labeling the CMC foliations in the context of quantum gravity. Roser's dissertation makes this plain as a pikestaff: "Despite decades of inquiry an adequate theory of ‘quantum gravity’ has remained elusive, in part due to the absence of data that would guide the search and in part due to technical difficulties, prominently among them the ‘problem of time’. The problem is a result of the attempt to quantise a classical theory with temporal reparameterisation and refoliation invariance such as general relativity."
Continuing: "In this thesis we argue that a foliation into slices of constant extrinsic curvature, parameterised by ‘York time’, is a viable contender. We argue that the role of York time in the initial-value problem of general relativity as well as a number of the parameter’s other properties make it the most promising candidate for a physically preferred notion of time."
A viable contender for what? For attempting to quantise a classical theory with temporal reparameterisation and refoliation invariance such as GR. Okay, so Roser's whole project (it seems to me) has to do with demonstrating how York time is the best prospect for a physically preferred notion of time when attempting to quantise GR. And at what point exactly would I want to do that? When would it even be relevant to do that? Well, it's relevant when the proper time of observers co-moving with the expansion of the universe (their clocks) can't be applied to a particular, quantum domain. The problem, though, is that conceptualizing the boundary between the quantum and the classical domains isn't (can't be?) what Linford needs it to be to make it relevant to the 2nd premise of the KCA. It's not as if the 'negative infinity' where York time places the singularity means that the singularity is an actually infinite number of, say, years away. That's just not what negative infinity means in this context at all.
(Roser does have a section in which he translates the two relevant Friedmann-Lemaître equations, "...usually expressed in cosmological time t or conformal time η, into the York-time description." This is actually very interesting because, if you do this, there isn't this strange barrier between time in the quantum era and time in the classical era. It's York time all the way down, so to speak. The translation is for checking ". . . the results of the reduction procedure.", the Hamiltonian reduction, to get rid of the 'awkwardness' of the Klein-Gordon equation [a result of the translation], which then provides more 'natural' equations [even if the resultant 'natural' equations are 'equivalent' to the equations without the reduction]. [Reducing the Hamiltonian is supposed to clear up a bulk of the problems you run into in 'canonical' Quantum Gravity models.] But at the conclusion of the chapter, it becomes evident that this doesn't have to do with reasons we need to prefer York to Cosmic time empirically. Roser admits that it all, "... depends on the existence of other evidence for York time as a physically fundamental time parameter. In this thesis we have argued that there are certainly are theoretical reasons. If dramatic progress is made in the development of some theory of quantum gravity that relies on York time, and observational evidence emerges that corroborates this theory, then this would be reason to take the extension seriously. Indeed it would be difficult to escape its necessity." So, by Roser's own admission, York time does not have observational evidence in its favor yet. All Roser is doing is offering theoretical reasons and these reasons come in part from doing the requisite mathematical translations. Given the state of play right now, empirically speaking, Cosmic time is the measure that wins out over York time.)
3.3. Taking a Closer Look at 'Negative Infinity' in York time
To reiterate, a CMC foliation carves spacetime in a 'series' of 3-d slices at varying 'instants' of time. Every slice geometrically represents the universe at that 'instant'. But you can label (parameterize) these slices differently. York time has absolutely nothing to do with metrics like 'seconds' or 'years'. Due to its mathematical abstractness, York 'time' focuses laserlike on the geometric properties of the changes in the 'mean curvature' of the foliations. York time's so-called progression is completely unrelated to the march of time in terms of seconds/years; it's about tracing changes in that curvature. Even here, you need constant vigilance against understanding the idea of 'changes' in terms of seconds/years. This isn't time as we understand it at all. To call York time 'time' at all can lead you astray conceptually rather easily, especially with its ideas of 'negative infinity', conjuring in the mind the kind of infinity philosophically discussed by Craig in the context of the KCA. So, the 'progression' or the 'change' of York time is not in terms of the passage of seconds/years, but in terms of the evolution of the universe you can measure by tracing the changes in the mean curvature of the spacetime slices. If the curvature changes, you're progressing through York time. York time parameterizes that 'progression' in a particular, mathematical way; it does it in such a way that a second of Cosmic time can be reparametrized as an infinite span of York time.
It's important to keep in mind that the CMC foliations don't themselves undergo any kind of change as you apply the different parameterizations. These foliations are ways to slice/carve spacetime. The changes happen when you parameterize these foliations in particular ways and it is these parameterizations that are the labels. Call them the Cosmic labels and the York labels. Thus the Cosmic label can parameterize these foliations in terms of a 'snapshot' of cosmic expansion 'per second' or 'per year' such that the regress of such seconds/years is ineluctably finite. AND, the York label can parameterize the foliations in terms of a 'snapshot' of the CHANGES of the mean curvature. Do you see what's happening here? What's happening is that Roser is making room for the idea that the York label can parameterize a FINITE INTERVAL (second/year, or a Planck era) in terms of the 'negative infinity of York time'. Hints of this kind of 'slight of hand' become more evident when you notice that Linford (and Roser, but Roser isn't in the relevant polemical context) eases into York time by first introducing Misner's time parameter. Thus, Roser:
In 1969 Misner proposed that the quantity − ln a — or (more or less equivalently) the logarithm of the temperature in the homogeneous approximation — would provide a time parameter with which to give an account of cosmic history that is more adequate than the conventional cosmological time t [85]. The new parameter would avoid the absurdly small numbers needed to describe early epochs. Misner wrote: ‘The universe is meaningfully infinitely old, since infinitely many things have happened since the beginning.’
First, notice how irrelevant all of this is to the second premise of the KCA. All that's required is that the empirical evidence makes it more plausible (probable) than not that the universe began to exist around 13.8 billion years ago, where the 'year' is the cosmic metric arbitrarily chosen to measure its finite duration. This has absolutely nothing to do with whether or not another time parameter can 'more adequately' describe the 'early epochs' by avoiding 'the absurdly small numbers' involved in such descriptions. Grant that superior parameter in the context of the superior adequacy of providing such descriptions. This doesn't have anything to do with whether or not the universe is around 13.8 billion 'years' old. Avoiding the small numbers is completely irrelevant as to whether there was an 'early epoch' and whether such an epoch had a finite duration. It's like saying whether you can deny that a foot-long ruler isn't a foot long because the back edge of the ruler, on a quantum level, can't be measured by inches, centimeters, and millimeters. Adopting another metric to describe that level isn't a rival to a metric that measures the ruler as a foot long.
Second, notice how you can distort what Misner is saying to make it look like he's saying that the universe isn't 13.8 billion years old, that it's actually an actually infinite number of years old, which isn't what Misner is saying at all when he's saying the universe is 'infinitely old'. I find the language used here extremely irritating, as irritating as the way Krauss uses the word 'nothing'. Arguing that because an infinite number of things have happened since the beginning doesn't mean that the universe is 'infinitly old' in the relevant sense, the sense in which it needs to have to subvert KCA's second premise.
Next we have this from Roser: "In terms of York time it is the early history that takes up the longest period ∆T. In fact, just as in the case of Misner’s parameter − ln a, the ‘beginning’ lies in the infinite past and unlike in the conventional description in terms of t there is no notion of ‘before the Big Bang’. The Planck era stretches from T = −∞ to just before the onset of inflation. Recent data [96] leads to an upper bound on the Hubble parameter during inflation of 3.6 × 10−5MPl (me: Pl is a subscribt), so that in reduced Planck units (where MPl = 1) this number also gives a rough estimate of T .
Sure, according to York time, the 'beginning' lies in the infinite past. But this is only from the perspective of the York time parameterization! The York metric takes extremely short intervals (like the Planck era) and 'stretches' them out so that there can be a mathematical description of each change on the foliations of the constant curvature. An infinite number of such changes correlates with properties of actual intervals of finite duration (seconds, years, Planck eras, etc.). So, it's simply irrelevant in determining whether or not the universe is probably 13.8 billion years old or an actually infinite number of years old. As Roser says: "... periods of large T-duration are of short t-duration and vice versa."
3.3. Linford's Two Technical Asides and York Time
I think we can apply the points made in 3.2 here to Linford's two technical asides. These asides are where I'll be setting up my response when he 'returns to regular programing' in his section 3.2.
3.3.1. The first technical aside has to do with Symmetry Breakers, the Probability of Conjunctions (probability of A&B = the probability of A times the probability of B/A), Boundaries of Probabilities (0 to 1), the Epistemic Probability of an Argument's Conclusion (it can't be any higher than the least probable premise of that argument), and how these relate to the acceptance of York or Cosmic time as representative of Absolute Time (and how one or the other will imply the universe being finitely or infinitely old).
If the probability that absolute time is approximately measured by cosmic time is 51% and by York time is 49%, and another independent premise of an argument has a probability of 80%, then the overall probability of the conclusion of that argument can be less than 50% (specifically, 40.8%).
But, first, if Cosmic and York time were simply two different parameters for describing the same Cauchy surface in a globally hyperbolic spacetime (i.e., an identical CMC foliation), then this argument would be significantly neutered. The two measures wouldn't be in competition with each other but would rather offer alternative ways to describe the same thing. Temperature remains the same whether you describe it in terms of Fahrenheit or Celsius, as does Distance, whether in miles or kilometers, as does Weight, whether in pounds or kilograms. The CMC foliations can remain an approximation to Absolute Time, while Cosmic and York Time are different, non-competing ways to label that foliation depending on your purposes. In this case, providing symmetry breakers would be a category error. That I tried to provide these in my first response bespeaks my ignorance.
But let's suppose symmetry breakers were relevant: is Linford fleshing out symmetry breakers in the context of conditional probability in vacuo, or is he attempting to describe the relevant probabilities and the role they play in symmetry breakers in terms of Bayesian analysis? It is a kind of subjective probability, so it seems to be a Bayesian analysis of conditional probability, I think. If so, not only would this be impotent against those who don't share Linford's priors, but he doesn't detail everything that's relevant for doing a Bayesian analysis. You don't only multiply the probability of a conjunct A (in A&B) by the probability of B/A.
Without going into too much detail, let's assume Linford is proffering mere conditional probabilities, norms for how to update your probabilistic beliefs given your other, related probabilistic beliefs. If that's the case, this is just a mathematical truism: the probability of a conjunction A&B is affected most by its least probable component. Sure. But while this observation is mathematically sound, it's trivial and it doesn't fully capture the nuances of how beliefs are updated in the real world, where multiple factors, including evidence and prior beliefs, play a role. There's more to the picture than Linford's first technical aside provides. It may provide the mathematical skeleton but the blood and sinews are missing. And that's where a Bayesian consideration might become relevant.
Finally, this first technical aside is no mystery to Craig. He discusses it here for anyone interested.
3.3.2. What about the second technical aside?
First, Linford corrects my mistake that York time gets rid of the Big Bang singularity altogether. It does, indeed, relegate that singularity to negative infinity. But I think the source of my confusion stemmed from the idea that earlier in the blog Linford, in his second reason for thinking that his schema can't be satisfied, admitted that 'most physicists doubt that singularities are real features of our world'. But if singularities are not real features of our world, then what is it that is relegated to negative infinity? Linford admits, in his correction, that his 'job would be really easy' if 'York time somehow removed the Big Bang singularity without relegating' it 'to negative infinity' since it would then 'only be a [sic] artifact of a notational choice and not a real feature of the world'.
But what is it that isn't a real feature here? I already specified above that Craig admits that it isn't a real feature when he said: "The initial cosmological singularity is a mathematical artifact of the standard model. I take it to be an idealization. It's dispensable. Cosmologists often cut out the initial singularity so that the universe, though finite in the past, has no boundary point." So, it's hard to see what Linford is implying about York time and how if York time has the Big Bang singularity relegated to negative infinity, that this somehow means that such a singularity is a real feature of the world. But if Craig denies that the singularity is a real feature of the world, then why is it that Linford's correction involves the idea that if York time's does relegate the singularity to negative infinity, then this also means that the singularity is a real feature of the world such that if it weren't a real feature of the world, then Linford's 'job would be really easy'? Perhaps because he thinks that it would be a short step toward demonstrating that his schema isn't satisfied? But there has to be more to it than that since Craig also doubts that singularities are real features of the world and still tentatively and realistically subscribes to FLRW models, which means that Craig would think that such models are 'approximately true within some domain'. The singularity, as a mathematical artifact, would realistically describe such a domain without ontologically commiting itself to this abstract object singularly referenced by 'Big Bang singularity'.
Linford then launches into a helpful mathematical explanation as to why the singularity, with York time, is relegated to negative infinity. It is here that I want the reader to pay special attention since it is here that I become very confused about why Linford goes on later to deny my accusation that Linford is 'trading on an ambiguity' and even more baffled as to why Linford thinks that I completely misunderstand 'what friends of the view that York time is absolute time' say, namely, that 'the duration of past York time can be subdivided into isochronous intervals and it is with respect to those intervals that the universe is infinitly old.' Let me hold the reader by the hand and show them the source of my confusion and bafflement.
So, per this mathematical explanation, let's break down exactly how and where York time relegates this singularity to negative infinity. First, focus on the relation between York time and Extrinsic Curvature. Every hypersurface in the CMC foliation has York time being proportional to the average value of the extrinsic curvature of such foliation. This average value is K. I get K by finding its trace. (You get the trace by summing over K with [the inverse metric tensor]. That tensor then becomes a scalar. That scalar represents K's trace.) And then that trace gives you the average value of K, extrinsic curvature, the curvature that York time T is working with. T is proportional to the trace of K. In FLRW spacetime, the trace of the K is inversely proportional to the Hubble parameter H, which is what describes the rate of the expansion of the universe. You define H by getting the ratio of the time derivative of the scale factor a to the scale factor itself. And here is a key point: the scale factor a gives a measure of the relative expansion of the universe. As one goes back in time towards the Big Bang, a becomes smaller, approaching zero.
If a (the scale factor) decreases toward zero, and it's in this sense that York time T tends to negative infinity, then how in the world can the past duration of T be evenly divided into isochronous intervals, especially if the universe is to be infinitely old in York time? The only way this can be resolved is if the intervals of T (York time) do not necessarily correspond linearly with the physical events or changes in the universe. In other words, they do not strictly correlate with the passage of a quantifiable collection of moments, like seconds or years, as typically understood, and as Cosmic Time would conceive of these kinds of duration. York time, in relegating the Big Bang to negative infinity, is essentially stretching out the time duration infinitely. The further back you go, the longer each physical "moment" gets stretched in York time, and so, even if each interval of York time is equal, what it represents in terms of physical events or changes in the universe won't be equal. So, it does seem apropos to raise the question of how isochronous intervals in York time can represent an ever-decreasing scale factor a.
So, keeping the isochronous point in the background, what happens as we approach the Big Bang and how does negative infinity come up? Well, you approach the Big Bang (i.e., as a goes to zero), and assuming that ȧ remains finite (where ȧ is that time derivative of the scale factor), the ratio ȧ/a shoots up to infinity! But how would it go to negative infinity? By negating ȧ/a. And by negating ȧ/a, T (York time) also goes to negative infinity. So, under the York time description, as we trace back to the beginning of the universe (the Big Bang), the time becomes more and more negative without bound. But since negative infinity isn't a defined point, this implies the Big Bang singularity doesn't have a defined beginning in York time. And so York time removes this definite starting point of the Big Bang singularity and pushes it to negative infinity.
But all of this is completely consistent with the idea that, per Cosmic time, the universe is 13.8 billion years old, that 100 billion years ago, it would not be true to affirm that the universe began to exist, and that therefore the universe would not have existed. And so it's extremely difficult for me to deny that Linford is not only trading on the noted ambiguity, but that he's playing fast and loose with the descriptive "infinitely old universe'. Nothing of Natural Theological relevance is broached when appealing to York time. The second premise of KCA is left in tact. York's time is absolutely and seamlessly and harmlessly consistent with the universe being 13.8 billion years old. The universe's singularity can be pushed to negative infinity and it also be the case that the universe be 13.8 billion years old! 'Negative infinity' does not mean 'infinitely old in the relevant sense', the sense in which it could be said that the universe is an actually infinite number of years, or minutes, or decades (pick your equal, non-zero, arbitrary, finite interval) old.
One wonders how Linford came to think York time would ever be a threat here. Not only is it consistent with the Cosmic time description, but because they are consistent, they aren't rivals when approximating Absolute Time in the ways that they do (a detail I'll get to below).
Keeping this in mind, certain turns of phrase begin to jump out at you that betray Linford's misunderstanding of York time. Consider this one: "Perhaps, some readers will object, even if the Big Bang is placed in the infinite past, the Universe, so depicted, would still have a beginning. Perhaps they imagine that the Big Bang is the Universe’s beginning and so the Universe would have a beginning no matter how long ago the Big Bang took place. A beginning that takes place infinitely long ago is still a beginning. But this objection is no good." What does Linford mean by 'how long ago'? If it's in terms of York time, we saw that this has nothing to do with years, seconds, decades, or any other equal, arbitrary, non-zero, finite interval as Cosmic time might conceive! This conflation is ubiquitous in his blog descriptions. Linford's 'line analogy' becomes virtually irrelevant when you see that this conflation is what motivates it. But even in Linford's formulation of the 'line analogy' you can see these turns of phrase.
The Line Analogy is supposed to show that my understanding of the universe's beginning might differ based on my chosen time framework. It considers an infinite real number line and a finite segment between 0 and 1 and then strips both of the numerical labels. Without labels, these two entities, despite their original differences in length (infinite vs. finite), become topologically indistinguishable, both having no clear starting or ending points. Similarly, my understanding of the universe's beginning can vary based on the time measurement framework I adopt, be it Cosmic time or York time. Thus, the inherent structure of something remains constant, but my perception can shift based on my method of "labeling."
Consider this from Linford and take note of where it's italicized: There is a strong intuition that if time is like the interval from 0 to 1, then time has a beginning, but if time is like the entire real line, then time has no beginning. Singular Big Bang models are like the interval from 0 to 1 in that the singularity is an open boundary; each point in the interval can be taken to represent a hypersurface in a CMC foliation. Thus, whether singular Big Bang models depict the Universe as having a beginning apparently depends upon how we label the hypersurfaces in the preferred foliation. If absolute time is correctly identified with cosmic time (or if one is a close approximation of the other), then the Universe (barring other objections) has a beginning. But if absolute time is instead identified with York time, then the Universe is beginningless.
Now, based on everything that's been discussed so far, how am I to understand the turns of phrase 'has no beginning' or 'the Universe is beginningless' when conceived in light of York time? Well, first, if one of Linford's goals is to argue that, just as in the line analogy, where the removal of numeric labels makes it impossible (without labels) to isolate a point at which the line 'begins', York time is supposed to render time, in some sense, as some kind of continuum. This is supposed to illustrate how the beginninglessness of the universe follows upon the extinguishment of some 'beginning' or 'starting' point.
I won't dwell too long on this idea because there is absolutely no way Linford is unaware of Craig's polemic against the notion that the only way the universe has a beginning is if it has a beginning point. This has been discussed so many times in numerous different publications, that it would be needlessly pedantic for me to point them all out. It is worth pointing out that this is also related to York time relegating the Big Bang singularity to 'negative infinity', which is supposed to suggest (among other things) that such a singularity isn't a finite point, stretching indefinitely into the 'infinite' past. So, it also seems to be intimating that if the universe doesn't have such a singularity, and this singularity doesn't mark a beginning point, then the universe is beginningless.
But, again, as we saw above, the idea of the universe being "beginningless" in York time doesn't mean that there was an infinite series of events before what we call the "Big Bang." It's more of a conceptual/theoretical framework where the initiation point of the universe (the Big Bang) doesn't have the same definitional boundary as it does in other interpretations. Of course, while I don't see the Big Bang as marked by a singular point, I don't deny that the Big Bang is a distinct, initial event. But York time gives me a different conceptual understanding of that same singularity.
So, my point is that Linford has front-loaded York time with turns of phrase that make it sound as if 'negative infinity' or 'infinitely old' or 'time having no beginning' or 'the Universe is beginningless' means the Cantorian idea having an infinite regress of isochronous temporal intervals (non-zero, finite, equal, and arbitrary intervals like seconds or years) when York time doesn't mean this at all. As we saw above, an interval of Planck time could correlate with an 'infinite' York interval for goodness' sake. If that's the case, how is this even remotely relevant to KCA's second premise?
3.4 My 'Birth-Analogy' and Reframing 'The Ambiguity' Linford is Trading On
Let's use these points as an opportunity to stop and address what Linford has to say in response to my original points about isochronous temporal intervals and the debate about whether Cosmic/York time is continuous/discrete.
I confess that my original point was misguided. I was trying to understand how York time approaches negative infinity and how such an approach is in sync with the scale factor of the universe approaching zero (discussed above).
But the problem is that I was still trying to understand this while still thinking that York intervals were at least similar to Cosmic intervals like seconds or years. This lead me to think that if the York intervals were not isochronous, then you might be able to extend the intervals that were not isochronous infinitely in a way that keeps the singularity a finite distance away in terms of yearly metric of 13.8 billion isochronous intervals.
Linford sums up my sentiments with my 'birth-analogy': "Damore apparently thinks that if we label the hypersurfaces in the CMC foliation with the York time, then the intervals will not be isochronous and so we will not be able to escape the verdict that the Universe had a beginning. He thinks that the sense in which the singularity is infinitely distant from the present is innocuous and irrelevant; Damore thinks this is the same sense in which my birth is infinitely distant from the present since I can “endlessly halve intervals separating my present existence from the date of my birth”. Had Damore been right, then the York time would be irrelevant for whether the universe is infinitely old, since the intervals considered would not be isochronous. But this is a complete misunderstanding of what friends of the view that York time is absolute time would say. They would say that the duration of past York time can be subdivided into isochronous intervals and it is with respect to those intervals that the universe is infinitely old."
Linford is correct as far as my erroneous 'isochronous-point' goes. The intervals of York time are definitely not not isochronous. So, my 'birth-analogy' is off-base if it's based on this faulty 'isochronous-point'. But based on my discussion above of Roser/Valentini regarding the notion of parametrization, my 'birth-analogy' retains its initial pedagogical value. It is, indeed, the case that, apart from my off-base 'isochronous-point', York time's placing the singularity at negative infinity is similar to putting my birth at negative infinity. Why? Because all York time is doing is REPARAMETRIZING a finite interval. Cosmically, that interval is measured by approximately 13.8 isochronous intervals called years. In my case, that interval is approximately 40 isochronous intervals called years. The two cases are nearly the same when you take into account the above discussion about classical and quantum regimes correlating not to two distinct periods of cosmic history, but two distinct levels of description of one period of such a history.
The spirit of this point is captured by something Linford says, but which it seems that Linford doesn't understand what this entails: "Obviously, isochronous intervals of York time are not isochronous intervals of cosmic time. But I don’t understand why this should matter. Friends of the view that York time measures absolute time would point out that isochronous intervals of cosmic time are not isochronous intervals of York time." The reason why it matters is isn't because of what I was saying regarding York time lacking isochronous intervals; it's precisely because York intervals are not Cosmic intervals! An infinite number of York intervals can be reparametrized as a finite number of (or even a single) Cosmic interval(s), which means that York intervals, by themselves, don't threaten KCA's second premise at all. The different intervals do not have to be rivals for parametrizing Absolute Time at all. And so they don't have to rivals in terms of specifying the finite duration of cosmic history. York's description of the early, early epochs of cosmic history reparametrize such epochs to uncover rich mathematical detail about such an epoch's foliation, detail left out by Cosmic intervals like a second or a year. But it doesn't follow at all that such Cosmic intervals cease to do the measuring that they do or that they cease to be the valid metric that they are. And so York intervals can continue to do the work that they do within a finite domain cosmically understood. We must constantly be vigilant against York intervals importing language from Cosmic intervals. There is no passage of York time, or, if there is, it's in a sense completely foreign to passage of years or minutes. And if it is, of what relevance is York time to KCA's second premise?
The only other relevant application is whether York time is a rival to Cosmic time in terms of measuring Absolute time; but if all York intervals do is reparametrize Cosmic intervals, these two modes aren't in competition at all. Agreed that Cosmic and York intervals aren't the same, and that isochronous Cosmic intervals don't correlate with isochronous York intervals. None of that is problematic. All of this undermines my earlier efforts to find so-called 'symmetry-breakers'. Such symmetry-breakers are misplaced in the context of two intervals providing their own parameters that don't exclude the applicability of the other in the appropriate domain. But this also undermines efforts to prop up one parameter is superior to another categorically as the preferred measure of Absolute time. This is captured by Linford's point that: "the York time and the cosmic time can be used to label one and the same CMC foliation. I think this was an issue on which Damore was confused, since he repeatedly writes about identifying the correct foliation instead of about identifying the correct labeling of that foliation." First, let me make a point about this supposed confusion. Linford is misinterpreting me here. When I speak about 'identifying the correct foliation', what I mean is getting clear about this 'correct labeling of the CMC foliation'. After all, without that labeling, I can't identify the 'correct foliation', where 'correct foliation' is going to be the CMC foliation we all agreed to make center stage. But, second, this point should be in the background of everything that's said above about Cosmic and York intervals being different, non-competing parameters for measuring Absolute Time. Note that such measures shouldn't understood to mean that Cosmic and York intervals measure Absolute Time without the mediating CMC foliation such intervals are supposed to correctly label. But all this means is that Cosmic and York intervals are different, non-competing parameters for labeling the CMC foliation.
In light of this, Linford's point here is largely moot: "In FLRW spacetimes where the CMC foliation is unique, there is a bijective map between the cosmic time and York time. Why? Precisely because every CMC hypersurface labeled by cosmic time is also labeled by York time. Any three dimensional cross section of an FLRW spacetime identified as an instant of cosmic time will also be an instant of York time and vice versa. For that reason, any argument for the identification of absolute time with cosmic time that counts only in favor of the CMC foliation will not be adequate for preferring York time over cosmic time." The CMC foliation was never supposed to be adequate for preferring York over cosmic time since, as was argued above, York and cosmic time are two different, non-competing parameters for labeling that foliation. The CMC foliation isn't for adjudicating between York and cosmic time; it's for approximating a measure for Absolute Time.
(A final point 'universal reference frames'; Linford: "Since, strictly speaking, one cannot generally define a universal reference frame in a General Relativistic context, I think Craig should be charitably read as defending a preferred foliation." I can't make sense of this. In a purely General Relativistic context, sure. But this is to view theory, once again, in abstraco, divorced from empirically discerned considerations of the universe's matter/energy distribution. Craig is explicit about this here: "Thus, it is possible to single out on physical grounds-not from the theory alone, but from de facto material conditions in the universe---a special group of preferred observers, the fundamental observers, that serve to define a privileged cosmic time, which deserves to be called the real cosmic time in counter distinction to other mathematically possible functions. Nor does this conclusion in any way clash with GR. That theory does not, pace Kroes, succeed in establishing the equivalence of all observers from a physical point of view, as we have seen, and there simply is no General Principle of Relativity that requires that no privileged time exists from the cosmological point of view. (221, God, Time, and Eternity)" Craig then supports this point with 2 sub-arguments, the second of which explicitly mentions 'preferred reference frames': the cosmological fluid, the microwave background radiation, and the quantum mechanical vacuum (quantum electrodynamics, EPR experiment and Bell's Inequalities), which are supposed to be reasons for reconsidering a 'modern aether', a universal, privileged reference frame, not only a preferred foliation.)
4. Linford's 5 Reasons for York time Approximating Absolute Time and My Symmetry Breakers.
Here I'll present Linford's reasons and show, based on the above, how they misconceive the relationship between York and cosmic time, and the relationship both metrics have to the CMC foliation. I'll also briefly discuss my proposed symmetry breakers, but show that my proposals presumed the same sort of misconception.
1st reason - I can't choose cosmic over York time because it's a labeling of the CMC foliation. They both do that. I don't dispute this. Did Craig argue this? Being York or cosmic time is a sufficient condition for labeling the CMC foliation, but each, taken individually, isn't necessary. But notice that if York and cosmic time aren't rivals in the way specified above (section 3), pointing this out misconceives the relationship they have to each other and the way they relate to the CMC foliation. They are different, non-competing parametrizations of the CMC foliation. They have different areas of focus and perform different functions relative to their domains of applicability.
2nd reason - I find this reason problematic. First, despite being a minority position, I'm not so sure that presentist time travel can be so breezily dismissed. The 'nowhere to travel to' objection has been addressed in a number of publications. But leaving that aside, I deny that the 'future' needs to 'exist' for it to be a spacetime where such a future can be predicted. Since the presentist can use 'spacetime' as geometrically represented on a diagram to map the mathematical relationships between the succession of the relevant hypersurfaces, such diagrammatically represented spacetimes are open for the presentist to solve initial value problems just as robustly as spacetimes that ontologically commit themselves to the existence of such a 'future'. Second, Linford discusses globally hyperbolic spacetimes, Cauchy surfaces, and their role in understanding the evolution of spacetime, and relates these to the CMC foliation, which York time labels. But none of this excludes cosmic time from its domain of applicability. Yes, in some Quantum Gravity proposals and when there's the Hamiltonian formulations of GR, York time would be superior to cosmic time in that domain of applicability, the quantum gravity regime. No problem. This would be a local, mathematical reparametrization of that particular granular domain, an awesome benefit for being able to label the CMC foliation in that domain. Cosmic time is way too rigid and clunky to apply to the perturbations of such quantum foam. Linford noting that cosmic time doesn't have a connection to the Hamiltonian formulation of GR and so doesn't play a corresponding role in any quantum gravity proposal is immaterial to my previous point about the two metrics being two non-competing parametrizations of the same foliation in their own domains of applicability.
3rd reason - Linford repeats the point about spatiotemporal regions beyond our cosmological horizon, which I responded to above. There is also a repeat of the point about York time being defined for a broader class of spacetimes than cosmic time, but I came away from this disagreeing with Linford's justification. But, mostly importantly, this reason illustrates my point about complimentary parametrization perfectly. Linford points out that York time has more mathematical dexterity when it comes to labeling those aspects of our observable universe that don't perfectly align with the ideal constraints of isotropy/homogeneity of FLRW spacetimes. For those parts that don't so perfectly align will be those parts that can be added to York time's domain of applicability; cosmic time labeling wouldn't be excluded due to its ambition of only being the approximation it claims to be. This makes the York labeling superior at these local pockets of anisotropy/heterogeneity, along with the quantum regimes mentioned above. If the two labelings are two non-competing parametrizations of the same foliation, there's nothing awry about selecting the labeling that has the universe's age at approximately 13.8 billion years. There would be something amiss if the 'negative infinity' of York time meant something relevant. But it doesn't, as I argued above. These same points can be applied to Linford's arguments from inflationary cosmology. Regarding the regions beyond our cosmological horizon due to inflation, this will be another domain of applicability for York time and the foliations it labels in these domains. Would this give us any reason to think that the universe is past-eternal? None that I can see. Would any of this undercut the underlying principle of dual parametrizations of the same CMC foliation? None that I can see.
4th reason - Here, Linford mentions the idea of 'stretching' 'time' (I put 'time' in scare quotes for a reason the reader should be aware of), which I noted above. But the issue is how to conceptualize this 'stretching' and whether or not it's the kind of stretching that is incompatible with cosmic parametrizations of foliation. And it doesn't seem to me. The stretching is a consequence of applying the York parametrization 'close to the singularity'. There is no problem here for me at all. If physicists find it useful to label the foliations close to the singularity with York time, this will be an additional domain of applicability where the foliations labeled can be parametrized in their respective ways. The idea that a 'second' of cosmic time could correspond to some 'tick' of York time might mean that the measurements are different, but it wouldn't mean that each measurement wouldn't parametrize the foliation in the particular way they do. And so they wouldn't exclude each other as potential labelings of the same foliation.
5th reason - Linford argues that York time would be preferable if attempting to formulate a hidden-variable quantum cosmology, and since Craig seems to favor Bohmian mechanics and absolute simultaneity, this could provide another reason for him to favor York time as a physically fundamental time parameter. But again. This also assumes the two parametrizations are exclusionary as labels of the same foliation. But most importantly, Linford repeats the misleading idea that York time puts the singularity to 'past infinity' when, as section 3 when into, the way York time understand 'negative/past infinity' isn't anything relevantly similar to what it needs to mean for the universe to be past-eternal or an actual infinite number of, say, years old.
Linford admits he's not presenting these reasons because he's convinced by them; he's presenting them because he wants partisans of cosmic time to rule York time out with something more than the simple idea that it labels the CMC foliation. That's understandable. But I think I've shown that because there's nothing about York time that excludes the approximate ambitions of cosmic time, the fact that Craig appeals to cosmic time as a candidate labeling of the CMC foliation isn't out of bounds. Cosmic is a sufficient condition for approximating those aspects of the CMC foliation it seeks to label. And because you can conceptualize these labels as non-competing parametrizations of different aspects of the CMC foliation, and so therefore have their domain of applicability, and because the idea of 'negative infinity' is misleading as it pertains to the mathematics of York time, that it doesn't have to do with the universe having a singularity that is an actually infinite number of 'years' distant from the present, I stand by the point that York and cosmic labels are complimentary parametrizations of the same CMC foliation, not exclusionary labels for different foliations. So, all these considerations, along with what I noted above regarding Roser admitting that even if the theoretical reasons favored York over cosmic time in the relevant domains of applicability, we still don't have observational evidence. Roser says this. So, the observational evidence we do have would seem to favor cosmic time in that label's domain of applicability.
On this note, we can now see the impropriety of the presentation of my symmetry breakers! I hadn't yet had the appropriate conceptualization of the dual labelings. Rather than justify the symmetry breakers, I'll just make some notes about what Linford said in his response.
1st symmetry breaker - This touches on Craig's argument that local physical clocks, which are (mostly) at rest with respect to the universe's expansion, seem to approximate cosmic time and hence could be measuring absolute time. Linford's response to this isn't compelling to me. He reiterates Poincaré's thought experiment, where apparent geometry differs from actual geometry, leading to skepticism about our ability to measure the world's true geometry. But the parity of the two situations is dissimilar. Craig's argument comes from P. C. W. Davies, "Spacetime Singularities in Cosmology and Black Hole Evaporations," in The Study 0/Time [II, ed. 1. T. Fraser, N. Lawrence, and D. Park (Berlin: Springer Verlag, 1978), p. 76. Davies says:
"At any given place in the universe, there is only one reference frame in which the universe expands isotropically. This privileged reference frame defines a privileged time scale (the time as told by a dock at rest in that frame). Two separated places have their privileged reference frames in mutual motion, because of the expansion of the universe. Nevertheless, the time measured by the entire collection of imaginary standard docks are obviously correlated such that the global condition (e.g. average separation of two galaxies) of the universe appears the same at equal times as registered by every privileged clock (assuming they are all properly synchronized). Happily, the earth is moving very slowly relatively to the local privileged frame in our vicinity of the universe, so that Earth time is a fairly accurate measure of cosmic time."
Craig commentates: "Thus, not only do we know that a privileged cosmic time in which the universe evolves exists, but because the earth is approximately at rest with respect to our galactic fundamental particle, we also have a fair idea of what time it is!"
This doesn't have to do with 'seemings', explicitly. I realize that Craig has phenomenological arguments, but this particular argument is based on empirical and observational aspects of cosmic time. The Earth moves very slowly relative to the local privileged frame, making Earth time a reasonably accurate measure of this cosmic time. Even if local clocks measure "physical time," those measurements may be close approximations of "absolute time" under specific conditions—such as being nearly at rest with respect to the privileged frame. Further, the empirical data related to Earth's position within the universal expansion provides a basis for approximating what "absolute time" might be; and it would be valid irrespective of the Neo-Lorentzian framework. If Linford has anxiety about how cosmic and York seemings are at loggerheads, perhaps this empirical element (along with what I've argued above about parametrization and Roser's comment) could settle one of the 'seemings' in the direction of particular domains of applicability, where each domain could be relativized to a respective York or cosmic labeling of the CMC foliation.
(I honestly forget the point I was trying to make about the Aristotelian view of temporal continua, so I'll drop that for now. I also have fallen away from being disposed toward treating York time instrumentally, though Roser's comment gives me pause. The point about global applicability can be dropped as it doesn't take into account dual parametrization. The point about the appeal to a broader range of spacetimes has been addressed, and the point about non-FLRW models is inapplicable to me, as are inflationary multiverses. Unfortunately, I'm sorry to say that I haven't able to retrieve the source where I read that a majority support cosmic time, so I'll have to leave the reader a promissory note on that. I do remember that source not making the explicit point that cosmic time is necessarily measuring Absolute Time, but I'll leave it at that. I don't dispute the role that York time plays in canonical quantum gravity; I do dispute that this is evidence that York time is a more viable candidate for representing "absolute time" compared to cosmic time, for reasons already given. And all of what I've offered wouldn't conflict with Linford's pointing out how the FLRW metric can also be expressed in terms of York time; in fact, it supports my point about dual parametrization of the same foliation. Hopefully, what I've offered here offers additional reasons for thinking that proper time of fundamental observers approximate Absolute Time rather than 'merely relying on what Craig asserts'.)
5. Skepticism and Neo-Lorentzianism
This should be quick. If all Linford is doing is adopting methodological skepticism to clarify why certain physical models (in this case, truncated spacetimes) are avoided, then that's fine. Of course, I don't want to extend intuitions to domains that are out of its reach and that need to be accessed with technical mathematics, etc. But I'm not sure I was making that point. If I was unclear, I apologize. If I recall correctly, all I was trying to argue in this sector is that, methodologically, I have a problem granting to mere possibility the power to subvert what seems to be the case. If extra reason is given for why intuition can't tread where technical reasons need to go, then that confirms what I'm saying: mere possibility isn't doing all the work to subvert my seemings. But I think any fallibilist worth their salt would agree that intuition wouldn't be a guide to truth in domains only accessible to more remote, technical means. The relevant frontier is variable.
Linford's point that Neo-Lorentzianism leads to skepticism about the experimental tests of SR and GR isn't entirely accurate to me. The empirical tests are interpreted in particular way, but based on what was said above, why can't the justification we have for thinking we're at rest with respect to our galactic fundamental particle also approximate to the experimental tests of SR and GR? Reference frames in motion relative to Earth, whether they be uniform or not, are discernible from Earth and so there's a way for the approximations of the SR/GR experimental tests to neutralize the charge of skepticism for me. I agree that Neo-Lorentzians argue that kinematic effects are a consequence of universal forces acting on objects that are in motion relative to an absolute reference frame. While I may not know my exact velocity relative to the universal frame, our physical laws and empirical observations might still provide a 'good enough' approximation for practical purposes. (On the other hand, as an aside, if all motion is relative and there is no preferred frame, why should we trust any frame's time readings as being "true"? Both theories, after all, do require us to abandon or modify some intuitive notions about time and space.) The point about the possibility of universal forces distorting my internal sense of time is, again, on the same footing (for me) as Matrix-type skeptical scenarios attempting to undermine my confidence in the reality of the external world. The extra piece of data is the empirical data supporting the idea about the Earth being approximately stationary relative to our galactic fundamental particle.
I'm not very moved by Linford's point about the anisotropy of the CMB radiation and the universal reference frame. Who argues that this anisotropy rules out GR? I don't. Does Craig? I can't find where. Linford's argument didn't interact with anything Craig said about the CMB radiation: "anisotropic for any observer in motion with respect to an observer whose spatial coordinates remain fixed. It is therefore a sort of ether, serving to distinguish physically a fundamental reference frame."; the tests that "...detect the earth's motion relative to the radiation background, thus fulfilling nineteenth century physics' dream of measuring the aether wind!"
Craig goes on: "Commenting on this result, Kanitscheider remarks, "The cosmic background radiation thereby furnishes a reference frame, relative to which it is meaningful to speak of an absolute motion.65 What Michelson and Morley failed to detect using visible light radiation, twentieth century physicists discovered using microwave radiation. Mansouri and Sexl comment, "The discovery of the cosmic background radiation has shown that cosmologically a preferred system of reference does exist. This system is defined and singled out much more unambiguously to be a candidate for a possible 'ether frame' than was the solar rest frame in Einstein's days."66 By means of this empirically distinguished frame of reference one can, in Stapp's words, "define an absolute order of coming into existence."67 One can only speculate whether, had this microwave background radiation and the measure of our motion relative to it been known to Einstein prior to 1905, he would have claimed that no fundamental frame exists relative to which all local inertial frames are in motion."
Footnote 68 (in God, Time and Eternity) is interesting: "Consider Arthur I. Miller's paper, "On Some Other Approaches to Electrodynamics in 1905," in Strangeness in the Proportion, pp. 66-91, in connection with P. A. M. Dirac's remark in discussion that:
"In one respect Einstein went far beyond Lorentz and Poincare and the others, and that was in asserting that the Lorentz transformation would apply to the whole of physics and not merely to the phenomena based on electrodynamics..., which is going far beyond what the people who were working with electrodynamics were thinking about. And, of course, in a way Einstein was wrong, because the Lorentz transformation does not apply to everything. There is the microwave radiation, which does provide an absolute velocity. It provides an ether, but the real importance of Einstein's work was to show how Lorentz transformations dominate physics" (p. A. M. Dirac, "Discussion," Strangeness in the Proportion, pp. 110-111)."
Cf. Nathan Rosen's comrnent:
"In view of the existence of the Hubble effect, it appears that the universe is expanding. It also appears that there exists a frame of reference-nearly coinciding with that of the solar system-in which the universe presents isotropic appearance. This holds for the Hubble effect and also the microwave background radiation. In other words there exists a fundamental frame in the universe. From the equations of the general relativity theory one can also show that, in such an expanding universe, an observer carrying out mechanical and optical experiments in his laboratory in principle can determine the motion of the laboratory with respect to this fundamental frame of reference.
One cannot help wondering what would have happened had Einstein been aware of the existence of this fundamental reference frame at the time he was looking for a generalization of the special relativity theory that would describe gravitation. Would he have developed the same general relativity theory that he actually did?" (Nathan Rosen, "Bimetric General Relativity and Cosmology," General Relativity and Gravitation 12 [1980]: 494.)
This doesn't mean that GR is incompatible with the anisotropy of the CMB. It means that Einstein may have formulated GR differently if he had been aware of it. But I digress. Linford's remaining points attempt to exploit the misconception of York and cosmic time as they relate to each other and the CMC foliation dealt with section 3, but there is also a kind of summing of a number of points that are strikes against the Neo-Lorentzian approach to Relativistic Cosmology. Some of his points seem to help me with the charge of skepticism. For example, the uniformity of universal forces affecting matter in the same way could entail that clocks that consistently don't measure "absolute time" mean that such consistency in deviating from such a measurement implies not being in uniform motion relative to Earth's motion relative the galactic fundamental particle.
The idea that Neo-Lorentzians leave as mysterious such 'universal forces' is a feature of a cost/benefit analysis that all interpretations of the Lorenz Transformation Equations have to deal with. Neo-Lorentzians pride themselves with having a causal explanation of the kinematic effects; early-Einsteinians make them completely inscrutable; Minkowskians have to handle the extravagant ontology implied by spacetime realism (and all the objections that could be raised against it). Each view has to swallow some cost to reap the interpretation's benefits. I may have to get to this in another blog, but Linford desires that the Neo-Lorentzian provide their own rigorous mathematical equations to provide a theoretical framework for the 'universal forces'. But even if that hasn't yet been provided, I'm sure there are Neo-Lorentzian research programs that have this a goal. On another hand, the Lorentz Transformation Equations seem sufficient for mathematical description, while the physical interpretation of that formalism involving universal forces could be a feature of that physical interpretation, and thus metaphysical (or something that is derived via a metaphysical inference) and so maybe not amenable to mathematical description. On yet another hand, I think it would make this blog a longer slog than it already is, but some philosophers of physics have crafted equations for SR/GR that don't invoke spacetime. I'll try to get to the details of this in a later blog. These equations do away with the four-vector altogether and make the entire formalism algebraic/analytical (but even if the geometrical equations are kept, the neo-Lorentzian can still keep from ontologically committing herself to spacetime). This involved the complete abandonment of the stress/energy tensor, by the way (among other things that escape me at the moment). In terms of simplicity of derivation, Craig notes how H.E. Ives derived the Lorentz Transformation Equations from the Law of Conservation of Energy and Momentum and the Laws of Transmission of Radiant Energy. I can't find where Linford discusses this. Finally, Linford bemoaning instrumentalism about GR misses what it is that Craig and I are instrumentalists about: not GR, but spacetime.
Conclusion
I abruptly end here. I really appreciate Dr. Linford taking the time to respond to me. I really do. Any discerned arrogance in this blog is entirely accidental. And I hope my ambition isn't outshined by any perceived rashness or recklessness in handling the material. I tried my best to study and research this for almost two years of my life now. I don't plan on stopping learning this subject when kronos has mercy. And from the bottom of my heart, I really do appreciate Linford's work in providing Craig's academic work to robust and sustained critique. I really learned, and will continue to learn, a lot! Blessings!

Hi Matthew --
ReplyDeleteI've read through your blog post and have begun drafting a reply. However, I'm not sure that this public back and forth is really the best format for our exchange. Can we come to a common understanding of what our respective positions are before writing another set of long and detailed blog posts?
I suggest that we schedule a time for a one-on-one meeting over a Zoom call. Please e-mail me at dlinford@purdue.edu.